Skew Heap

유용한 링크: 위키백과, Skew heap visualization, NTU 강의자료

 

Skew heap(혹은 self-adjusting heap)은 이진트리로 구현된 힙 자료구조다. 우리가 배운 기본적인 힙은 완전이진트리이므로 배열과 인덱스를 이용하여 편하게 구현이 가능하다. 그러나, Skew heap은 완전이진트리가 아닌 그냥 이진트리이므로 배열을 이용한 구현을 할 수 없다.

 

그렇다면, 일반 힙이 아닌 Skew heap이 필요한 순간은 언제일까? 바로, 서로 다른 두 힙을 하나로 빠르게 합치고 싶은 순간에 쓸 수 있다. 서로 다른 두 힙을 하나로 합치는 것을 merge 연산이라고 한다. Skew heap은 merge 연산 중간, 왼쪽 자식과 오른쪽 자식을 무조건적으로 바꿔주어 균형을 유지한다. 이 merge 연산은 Skew heap에 원소를 추가(push)하거나, 루트에 있는 값을 제거(pop)할 때도 사용된다. 힙이 균형잡혀 있기 때문에 merge 연산은 amortised $O(\lg n)$ 시간복잡도를 가진다. 좀 더 정확히 하자면, 황금비 $\varphi = \frac{1+\sqrt{5}}{2}$가 있을 때, $O(\log_{\varphi} n)$이 된다. 이는 약 $1.44 \lg n$이다.

 

Skew heap은 다음과 같이 정의된다:

1. 원소가 하나인 힙은 Skew heap이다.

2. 두 Skew heap을 merge한 결과는 Skew heap이다.

 

이제 두 Skew heap을 하나로 합치는 merge 연산이 어떻게 동작하는지 알아보자. Merge 연산이 하는 일은 다음과 같다:

1. 합치려고 하는 두 Skew heap 중 루트가 작은 것을 $t_1$, 나머지를 $t_2$라 하자. 그리고 만들려고 하는 새로운 힙을 $r$이라 하자.

2. $r$의 루트는 $t_1$의 루트가 되며, $r$의 오른쪽 서브트리는 $t_1$의 왼쪽 서브트리가 된다.

3. 재귀적으로 $t_2$와 $t_1$의 오른쪽 서브트리를 합쳐 하나의 힙으로 만든 뒤, 그 힙을 $r$의 왼쪽 서브트리로 둔다.

 

다음은 merge 연산의 예시이다:

<그림 1> 합치려고 하는 두 Skew Heap

<그림 2> 합쳐진 결과

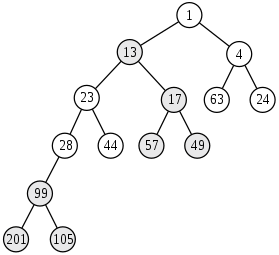
마지막으로, push와 pop은 어떻게 구현할 수 있을까? 원소를 삽입하는 것은 크기가 1인 Skew heap과의 merge로 구현할 수 있고, 루트를 삭제하는 것은 루트의 왼쪽 서브트리에 해당하는 Skew heap과 오른쪽 서브트리에 해당하는 Skew heap을 합치는 것으로 구현할 수 있다.

 

Skew heap을 C++으로 구현하면 다음과 같다.

#include <bits/stdc++.h> using namespace std; template<typename T> struct SkewHeap{ using value_t = T; struct Node; using node_t = Node; using nodeptr_t = unique_ptr<node_t>; struct Node{ Node() = default; Node(const T& value): value(value){} value_t value; nodeptr_t left = nullptr, right = nullptr; static nodeptr_t merge(nodeptr_t t1, nodeptr_t t2){ if (t1 == nullptr) return t2; if (t2 == nullptr) return t1; if (t2->value < t1->value) return merge(move(t2), move(t1)); nodeptr_t tmp = move(t1->right); t1->right = move(t1->left); t1->left = merge(move(t2), move(tmp)); return t1; } }; nodeptr_t m_root{}; size_t m_size{}; bool empty()const{ return m_size == 0; } size_t size()const{ return m_size; } value_t top()const{ return m_root->value; } value_t second_top()const{ if (m_root->left == nullptr) return m_root->right->value; if (m_root->right == nullptr) return m_root->left->value; return min(m_root->left->value, m_root->right->value); } value_t pop(){ --m_size; auto value = m_root->value; m_root = node_t::merge(move(m_root->left), move(m_root->right)); return value; } void push(const value_t& value){ ++m_size; m_root = node_t::merge(move(m_root), nodeptr_t{new node_t(value)}); } void merge(SkewHeap<value_t>&& other){ m_size += other.m_size; m_root = node_t::merge(move(m_root), move(other.m_root)); other.m_size = 0; other.m_root = nullptr; } };

 

Skew heap은 Hu-Tucker algorithm을 구현할 때 활용할 수 있다.