티스토리 뷰
길이가 $n$인 문자열 $s$가 있다. $1 \leq i \lt n$인 $i$에 대해 $z[i]$를 $i$에서 시작하는 suffix와 $s$의 가장 긴 common prefix의 길이라고 정의하자. 편의상 $z[0] = 0$이다. 이러한 $z$ 배열을 문자열 $s$의 Z-function이라고 부른다.
예를 들어, 문자열 "aaaaa"의 경우, $z = [0, 4, 3, 2, 1]$이 되며, 문자열 "aaabaab"의 경우, $z = [0, 2, 1, 0, 2, 1, 0]$이 되고, 문자열 "abacaba"의 경우, $z = [0, 0, 1, 0, 3, 0, 1]$이 된다.
Z-function을 $O(n^2)$ 시간복잡도로 naive 하게 구하면 아래와 같이 코딩할 수 있다.
각 $z[i]$는 0에서부터 시작하여, 6번째 줄의 while문을 통해 적절한 값까지 커져간다. 이때, 이전에 계산된 $z$ 값을 이용하여 $z[i]$의 시작 값을 0이 아닌, 다른 수로 정할 수 있다.
현재까지 prefix와 매칭된 부분 문자열 중에 끝점이 가장 오른쪽에 있는 부분 문자열을 $[l, r]$이라고 하자. 만약 $i \leq r$이라면, $z$의 정의에 따라 $z[i] \geq \min(r-i+1, z[i-l])$라는 것을 알 수 있다. 즉, $z[i]$의 시작 값으로 0이 아니라, $\min(r-i+1, z[i-l])$을 할 수 있다. 아래 그림을 참고하자.
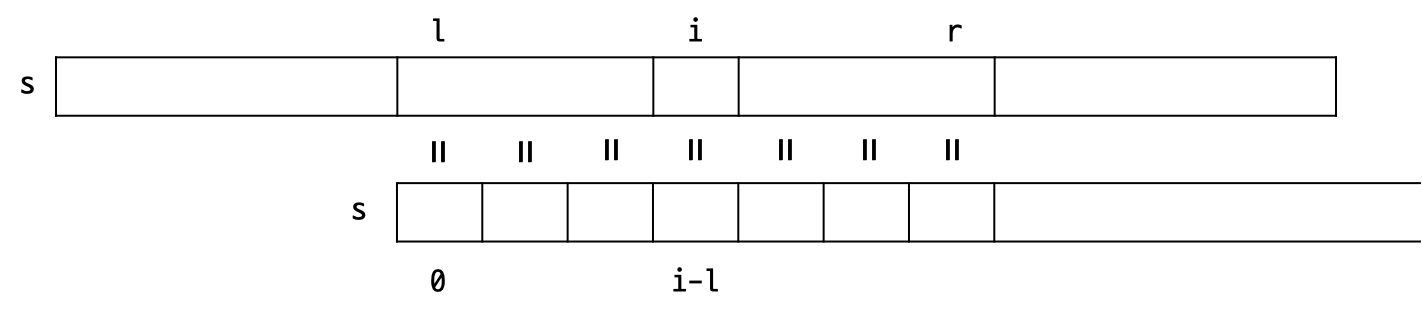
이를 적용하여 코드를 개선하면 다음과 같이 된다.
이 코드의 시간복잡도는 $O(n)$이다. 그 이유를 증명하기 위해 $i \leq r$인 상황의 어떤 $i$에 대해 $z[i]$의 초기값을 $z_0 = \min(r-i+1, z[i-l])$이라고 하자.
만약, $r-i+1 \leq z[i-l]$인 경우, $z_0 = r-i+1$이며 7번째 줄의 while문이 돌 때마다, 이후 $r$ 값은 하나씩 증가하게 된다.
만약, $z[i-l] \lt r-i+1$인 경우, $z_0 = z[i-l]$이 된다. 즉, 아래 그림과 같은 상황이다.
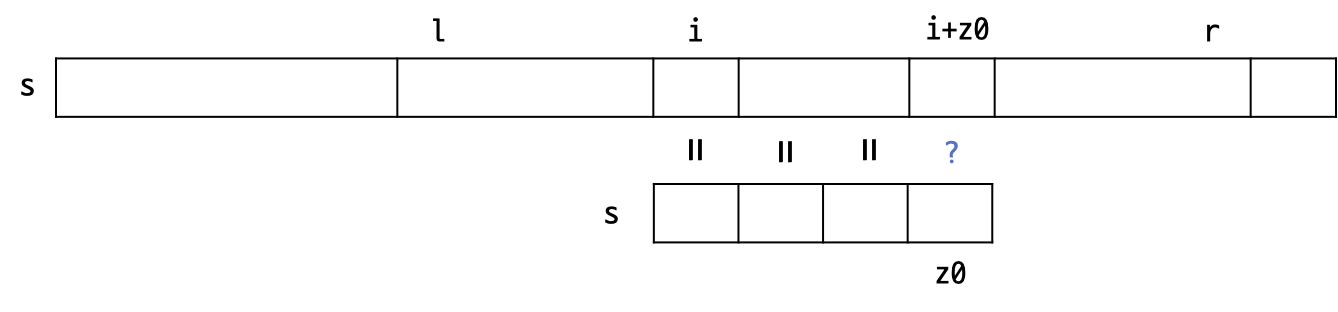
$z[i-l] = z_0$라는 것은 $s[z_0] \ne z[i-l+z_0]$라는 것을 의미하며,
$r = l+z[l]-1 \geq i+z_0$라는 것은 $s[i+z_0-l] = s[i+z_0]$를 의미한다.
즉, 항상 $s[z_0] \ne s[i+z_0]$다. 그렇기 때문에, 이러한 경우 7번째 줄의 while문을 돌지 않게 된다.
이러한 사실들을 통해, 7번째 while문이 돈다는 것은 항상 $r$값을 증가시킨다는 것을 의미하며, $r$의 최댓값은 $n$이므로, 이러한 증가는 최대 $n$번 일어난다는 것을 알 수 있다. 즉, 7번째 while문은 최대 $n$번 반복한다. 그러므로 전체 시간복잡도는 $O(n)$이다.
일반적으로 Suffix Array를 통해 $O(n \lg n)$ 시간복잡도로, Z-function을 구할 수 있기 때문에, Z-function으로 할 수 있는 모든 것을 Suffix Array를 통해서도 가능하다. 다만, Z-function의 시간복잡도가 $O(n)$으로 조금 더 빠르고, 구현이 더 간단하기 때문에 활용 가치가 있다. 예를 들어, BOJ 13576 Prefix와 Suffix 문제는 Suffix Array로도 해결할 수 있지만, Z-function을 이용하면 더 빠르고 간단하게 해결할 수 있다.
'공부' 카테고리의 다른 글
| Hu-Tucker Algorithm (0) | 2022.05.03 |
|---|---|
| Skew Heap (0) | 2022.05.03 |
| Li Chao Tree (Dynamic Convex Hull Optimization) (0) | 2021.03.08 |
| Stern-Brocot 트리 (0) | 2019.05.21 |
| 트리의 지름 구하기 (375) | 2016.10.11 |
- Total
- Today
- Yesterday
- Boyer
- IOI2012
- USACO
- IOI2014
- TRIE
- vote
- dynamic programming
- Greedy Method
- IOI2013
- BOI
- ioi
- Dynamic Pramming
- moore
- idea
- Knuth Optimization
- Algorithm
- majority
- Splay Tree
- IOI2011
- Boyer-Moore Majority Vote Algorithm
- optimization
- Segment tree
- Parametric Search
- HackerRank
- BOI 2001
- Tree
- BOI 2009
- Dijkstra
- Divide & Conquer
- z-trening
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
