티스토리 뷰

해법

Nexon Youth Programming Challenge(NYPC) 2020 예선 풀이

전명우 2020. 9. 6. 23:27

1. S OR T

스페이스(S)와 탭(T)을 입력한 순서가 주어졌을 때, 총 몇 칸 띄어지게 되었는지 구하는 문제다. 단, 탭 크기는 4다.

 

문자열을 입력받아서 S가 나오면 칸 수를 1 늘려주고, T가 나오면 칸 수를 현재 칸 수보다 큰 4의 배수로 만들어주면 된다.

더보기

2. 카트라이더 별 모으기

3개의 별이 있고 각 별을 획득할 수 있는 기록 제한이 주어졌을 때, 주어진 기록이 몇 개의 별을 획득할 수 있는지 구하는 문제다.

 

이 문제에서 시간이 기록은 'aa:bb:cc'꼴로 주어지는데, 이 기록 문자열을 정수로 변환해도 되고, 정수로 변환하지 않고 문자열 그대로 사전 순 비교를 해도 된다.

더보기

3. 스피드전 할까 아이템전 할까

카트라이더의 팀전은 4:4로 진행된다. 이 문제에서 스피드 팀전은 팀원 실력의 합이 큰 팀이 이기고, 아이템 팀전은 팀원 실력의 최댓값이 큰 팀이 이긴다. 두 팀의 팀원들의 실력들이 들어왔을 때, 스피드전을 해야만 이길 수 있는지(S), 아이템전을 해야만 이길 수 있는지(I), 아니면 다른 경우인지(R) 구하는 문제다.

 

입력이 한 줄에 8개의 정수로 주어지는데, 앞 4개 정수의 합과 최댓값을 구하고, 뒤 4개 정수의 합과 최댓값을 구해 비교하면서 스피드전을 했을 경우 이기는지, 아이템전을 했을 경우 이기는지 구하면 문제를 해결할 수 있다.

더보기

4. 실력별 매칭

대기열에 $N$ 명의 유저가 있고. 대기열에 있는 유저들의 실력 점수 $R_i$를 알고 있다. 대기열에 새로 들어올 유저가 한 명 있는데, 이 유저의 실력 점수는 $S$다. 이때, 대기열에 있는 유저 중 새로 들어올 유저와 실력 점수 차이가 가장 작은 유저 $K$ 명을 구하는 문제다. 만약, 실력 점수 차이가 같은 경우 실력 점수 값이 작은 유저를 선택해야 하며, 주어지는 실력 점수는 모두 다르다.

 

대기열에 있는 유저를 $|R_i - S|$ 순서로 정렬하고, 만약 $|R_i - S|$가 같은 경우, $R_i$ 값을 기준으로 정렬한다. 이렇게 정렬한 뒤, 앞에 있는 유저 $K$ 명의 번호를 출력하면 된다.

더보기

5. 우승자 찾기

$N$ 명의 유저가 참여하는 카트라이더 시합이 열렸다. 모든 유저는 시작점에서 동시에 출발해서 정해진 트랙을 계속 반복하면서 주행한다. 출발 이후 한 바퀴를 돌아 다시 시작점으로 돌아온 유저의 번호를 모두 기록했다. 같은 시간에 시작점을 통과하는 유저는 없었다. 단, 유저의 번호만 기록되고 시작점을 통과한 시각은 기록하지 못했다. 베스트 랩 타임이 제일 짧은 유저가 우승자가 되는데, 우승자로 가능한 유저의 번호를 모두 구하는 문제다.

 

예를 들어, [1, 2, 3, 2, 1, 2, 3] 순서로 유저가 시작점을 지났다고 하자. 1번 유저는 맨 처음 시작점으로 되돌아왔으므로, 그 시간이 매우 짧은 경우 우승자가 된다. 즉, 1번 유저는 우승자 후보가 될 수 있다. 2번 유저도 우승자 후보가 될 수 있는데, 2번 유저가 두 번째 바퀴를 도는 시간이 매우 짧으면 우승자 후보가 될 수 있다. 3번 유저는 우승자 후보가 될 수 없는데, 첫 번째 바퀴를 도는 경우가 매우 짧은 경우를 고려했을 때 1번 유저의 첫 번째 바퀴 도는 시간이 더 짧고, 두 번째 바퀴를 도는 경우가 매우 짧은 경우를 고려했을 때 2번 유저의 세 번째 바퀴 도는 시간이 더 짧기 때문이다. 좀 더 자세히 말하면, 3번 유저가 두 번째 바퀴를 도는 사이, 시작점을 지나는 유저 순서는 [2, 1, 2]인데, 2가 두 번 등장하므로 2번 유저의 랩 타임이 3번 유저의 두 번째 바퀴의 랩 타임보다 좋을 수밖에 없다. 이런 관찰을 통해 문제를 해결할 수 있다.

더보기

6. 도토리를 주워라

다람쥐가 $N \times N$ 격자판 위에 있다. 1행 1열의 칸에서 다람쥐가 시작하여 N행 N열의 칸까지 가야 한다. 다람쥐는 왼쪽 방향, 오른쪽 방향, 아래 방향으로만 움직일 수 있다. 각 격자 칸은 비어있거나, 도토리가 있거나, 장애물이 있다. 이때, 가장 많은 수의 도토리를 주워 도착점에 도착하는 이동 커맨드를 구하는 문제다. 단, 도착점에 도착한 이후에도 더 움직여서 도토리를 더 먹고 도착점으로 돌아와도 된다.

 

이 문제는 실행 결과 제출형(Output only) 문제다. 그리고 문제 해결을 돕는 시뮬레이터가 제공되어 앞의 미션들은 손으로 해결하기 쉽다. 소스 코드를 작성하여 이 문제를 푸는 난이도는 다른 1일 차 공개 문제보다 아주 어려운데, 시뮬레이터 제공이 감안되어 1일 차에 쉬운 문제들과 같이 공개된 듯하다.

 

이 문제를 소스코드 작성으로 풀 경우 다음과 같은 풀이로 해결할 수 있다. 좌우로 연속하게 비어있는 칸들을 하나로 묶어 정점으로 표현한다. 격자판에서 위에서 아래로 이동할 수 있는 칸 쌍에 대해 방향성 간선을 추가한다. 이런 식으로 그래프를 그리면 사이클이 없는 방향성 그래프(DAG, Directed Acyclic Graph)가 된다. 정점마다 그 정점에 속하는 칸에 있는 도토리 수 합을 정점의 가중치로 둔다. 그러면 DAG에서 시작 정점과 도착 정점이 있을 때, 경로에 속한 정점 가중치 합이 가장 큰 경로를 구하는 문제가 된다. 이는 위상 정렬과 DP로 해결할 수 있다. 이 문제에서 정점을 만들 때, 격자판의 위에서부터 번호를 매겨주면 위상 정렬을 하지 않아도 된다. DP로 가장 많은 도토리를 주웠을 때 주운 도토리 수를 구할 수 있는데, 이 문제에서 요구하는 것은 다람쥐의 이동 커맨드다. 다람쥐의 이동 커맨드를 구하기 위해서 그래프에서 실제 경로가 무엇인지 구하고 그 경로를 다람쥐의 이동 커맨드로 만드는 후처리가 필요하다.

더보기

7. 난센스 퀴즈

숫자 A, B, C, D가 있을 때, A □ B □ C = D 식의 □ 칸에 +, -, ×, ÷, . 5개의 기호를 서로 다르게 넣어서 성립하는 등식을 만드는 문제다. 예를 들어, A=5, B=1, C=4, D=7이라면, 5×1.4=7과 같이 식을 만드는 것도 가능하다. 답이 유일한 경우만 입력으로 주어진다.

 

함수 인자에 있는 문자열의 코드를 그대로 실행해주는 Python의 eval 함수를 이용하면 문제 풀이가 매우 쉽다. 아래 코드를 참고하자.

더보기

 

만약, C++로 이 문제를 해결한다면 가능한 20가지의 연산에 대한 if문 코드를 만들어주는 코드를 작성해도 된다. 아래 코드를 참고하자. 아래 코드에서 주석 부분이 코드를 만들어주는 코드 부분이다.

더보기

8. 이어 달리기

$N$ 명의 유저가 있다. 각 유저의 기록이 주어진다. 두 명의 유저가 한 팀을 이루는데, 팀에 속하지 않은 유저가 있을 수 있으며, 한 유저는 여러 팀에 속할 수 없다. 팀의 기록은 팀에 속한 두 유저의 기록 합이다. 가장 기록이 좋은 팀을 기준으로 기록이 10초 미만으로 차이나는 팀들은 보상을 받는다. 이때, 보상받는 팀의 수가 최대가 되도록 팀을 배정했을 때, 보상받는 팀의 수를 구하는 문제다.

 

가장 기록이 좋은 팀의 기록을 정하면, 보상받는 팀의 기록의 범위가 정해진다. 이렇게 가능한 기록 범위는 $O(N^2)$개다. 각 기록 범위에 대해 그 기록 범위에 팀의 기록이 들어오도록 가장 많은 수의 팀을 배정하는 것을 $O(N)$ 시간에 하면 전체 시간 복잡도 $O(N^3)$에 이 문제를 해결할 수 있다.

 

기록 범위가 정해졌을 때, 그 기록 범위에 팀의 기록이 들어오도록 가장 많은 수의 팀을 배정하는 것은 정렬된 배열에서 two pointers algorithm을 이용한 욕심쟁이 기법으로 해결할 수 있다. 유저의 기록을 입력받은 직후 한 번만 정렬하면 정렬은 매번 할 필요가 없다. 즉, two pointers algorithm만 하면 되므로 시간 복잡도는 $O(N)$이다.

더보기

9. 몰이 사냥

$N$마리의 몬스터가 일차원 맵에 있다. 0 이상의 정수 $t$에 대해 시간 $t$에서 몬스터 $i$의 위치는 $d_i + t \times s_i$이다. 스킬의 범위는 $R$이다. 즉, 위치 $p$에 스킬을 사용하면 $p \leq x \leq p+R$인 $x$에 있는 몬스터는 스킬에 맞는다. 스킬의 사거리는 $X$이다. 즉, 위치 $p$는 $0 \leq p \leq X$를 만족해야 한다. 원하는 시간에 스킬을 원하는 위치에 사용하여 모든 몬스터를 맞출 수 있는지 여부를 구하는 문제다.

 

특정 시간에 모든 몬스터를 맞출 수 있으려면 모든 몬스터의 위치가 $0$ 이상 $X+R$이하이며, 가장 먼 몬스터 사이의 거리가 $R$ 이하여야 한다. 이는 필요충분조건이다. 몬스터의 위치가 선형으로 변하므로 모든 몬스터의 위치가 $0$ 이상 $X+R$이하인 시간의 범위는 연속하게 나오거나 존재하지 않는다. 존재하지 않는다면 답은 불가능하고, 시간 범위가 있다면 그 시간 범위 안에 가장 먼 몬스터 사이의 거리가 $R$ 이하인 경우가 있는지 확인해야 한다.

 

시간 $t$에 따른 가장 먼 몬스터 사이의 거리 $d(t)$를 그래프로 그려보면 아래로 볼록하다는 사실을 알 수 있다. 이에 대한 간단한 증명을 소개하겠다. 서로 다른 몬스터 $i$와 몬스터 $j$의 거리 $d_{ij}(t) = |x_i(t)-x_j(t)|$는 $x_i(t)$와 $x_j(t)$가 일차 함수이기 때문에 수평하거나, V자 모양이다. $d(t)=\max_{i, j} d_{ij}(t)$이므로 $d(t)$는 V자와 수평한 그래프를 그려놓고 그중 최댓값을 따라 그린 모양이 된다. 즉, $d(t)$는 아래 그림의 빨간색 선과 같이 아래로 볼록한 모양이 나온다.

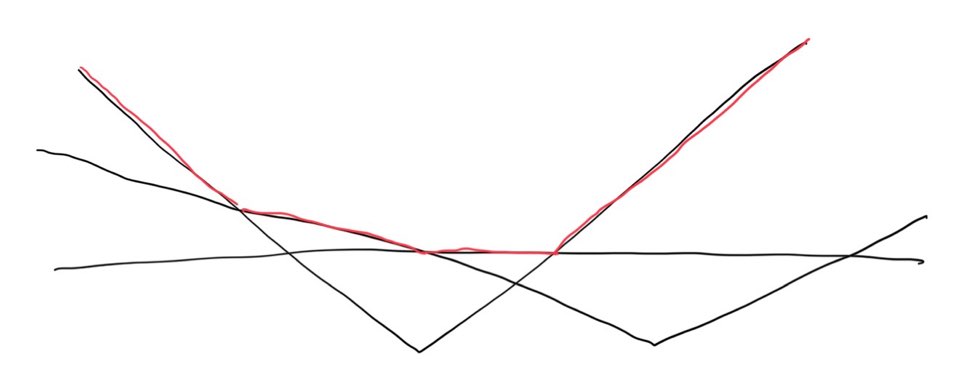
이 문제를 해결하기 위해 구해야 하는 것은 가장 먼 몬스터 사이의 거리 최솟값이다. 즉, 아래로 볼록한 함수에서 최저점을 구해야 하며, 이는 삼분 탐색(Ternary Search)으로 해결할 수 있다. 이 문제에서 시간 $t$는 정수만 고려해도 되므로, 실수 오차 없이 문제를 깔끔하게 해결할 수 있다.

더보기

10. 탐험 로봇

$R \times C$ 크기의 격자 판이 있다. 이 격자 판의 각 격자 칸은 육지이거나, 바다이거나, 알 수 없는 상태다. 상하좌우로 인접한 육지 덩어리를 섬이라고 부른다. 알 수 없는 상태인 칸에 적절히 육지와 바다를 선택하여 넣었을 때, 가능한 섬 개수의 최솟값과 최댓값을 구하는 문제다.

 

섬 개수의 최솟값을 구하는 문제와 섬 개수의 최댓값을 구하는 문제 두 개를 해결해야 한다. 섬 개수의 최솟값을 구하는 문제는 간단한 Flood Fill로 해결할 수 있다. 임의의 육지에서 시작하여 상하좌우로 인접한 알 수 없는 상태인 칸과 육지 칸을 방문하는 Flood Fill을 구현한다. 이때, 방문한 칸은 모두 육지로 선택하고, 방문하지 않은 칸은 모두 바다로 선택하면 섬의 개수가 최소가 된다. 시간 복잡도는 $O(RC)$가 된다.

 

섬 개수의 최댓값을 구하는 문제는 상당히 까다롭다. 2일 차 공개 문제 중 가장 어려운 문제다. 이를 해결하기 위해 몇 가지 사실을 생각해야 한다. 섬을 최대한 많이 만들기 위해, 육지와 상하좌우로 인접한 알 수 없는 상태인 칸은 바다로 만들고, 크기가 1인 섬들을 최대한 많이 만들면 된다. 크기가 1인 섬들을 최대한 많이 만들기 위해 격자 판을 그래프로 표현한다. 알 수 없는 상태인 칸을 정점으로 생각하고 상하좌우로 인접한 다른 알 수 없는 상태인 칸에 무방향 간선을 그린다. 이렇게 표현된 그래프는 이분 그래프인 것을 알 수 있다. 이렇게 그려진 이분 그래프에서 최대 독립 집합(Maximum Independent Set)을 구해 그 집합에 들어있는 정점에 해당하는 칸은 육지로 선택하고, 그렇지 않은 칸은 바다로 선택하면 크기가 1인 섬이 가장 많이 만들어진다. 모든 그래프에서 최대 독립 집합은 최소 정점 커버(Minimum Vertex Cover)의 여집합이고, 이분 그래프에서 최소 정점 커버는 최대 매칭으로 구할 수 있다. 이분 그래프에서 최대 매칭은 최대 유량(Maximum Flow) 알고리즘으로도 구할 수 있고, Hopcroft Karp 알고리즘으로도 구할 수 있다. 즉, 정점이 $V$ 개인 이분 그래프에서 최대 매칭이 $M$개라고 할 때, 만들 수 있는 크기 1인 섬 개수의 최댓값은 $V - M$이다. 이분 그래프의 최대 매칭을 Hopcroft Karp 알고리즘으로 구할 경우, 시간 복잡도는 $O((RC)^{1.5})$가 된다.

더보기

11. 격자 게임

3행의 격자 칸이 있다. 1행의 칸 수가 $A$이고, 2행의 칸 수가 $B$이고, 3행의 칸 수가 $C$인 상태를 $(A, B, C)$라고 표현하자. 두 사람이 번갈아 가면서 게임을 진행한다. 현재 상태가 $(A, B, C)$일 때, 각 턴마다 $i \lt A$인 $i$에 대해 $(i, B, C)$, $(i, i, C)$ 혹은 $(i, i, i)$인 상태로 넘어가거나, $A \leq i \lt B$인 $i$에 대해 $(A, i, C)$ 혹은 $(A, i, i)$인 상태로 넘어가거나, $B \leq i \lt C$인 $i$에 대해 $(A, B, i)$ 상태로 넘어갈 수 있다. 상태 $(0, 0, 0)$을 만드는 사람이 진다. 이렇게 게임을 진행할 때, 초기 상태에서 먼저 시작하는 사람이 되어 상대방을 이기는 동작을 구현하는 문제다. 초기 상태는 항상 먼저 이기는 사람이 필승 전략을 가질 수 있는 상태이다.

 

이 문제는 NYPC에서 처음 출제되는 대화형(interactive) 문제다. 대화형 문제로 일반적인 게임 DP 문제가 출제되었다. 일반적인 게임은 다음 설명할 DP로 해결된다. 우선 DP 배열 $D$의 정의는 다음과 같다:

$$D_{state} = \text{현재 상태가 }state\text{일 때, 필승 전략이 있으면 true 없으면 false}$$

게임 DP에서 점화식은 다음과 같다:

$$D_{state} = \sum {\neg D_{next\ state}}$$

즉, 현재 상태가 $state$이고 다음 상태로 가능한 것 중 하나가 $next\ state$인 경우, $D_{next\ state}$ 중 하나라도 $\text{false}$라면 $D_{state}$는 $\text{true}$가 되며, 그렇지 않다면 $\text{false}$가 된다. 좀 더 자세히 말하면, 나에게 필승 전략이 있는 상태라는 것은 상대방에게 필승 전략이 없는 상태를 만들 수 있는 상태인 것이며, 상대방에게 필승 전략이 없는 상태를 계속 만들어주면 결국 이긴다. 이 문제에서 상태 $(0, 0, 0)$을 만드는 사람이 지는 것이므로, 상태 $(0, 0, 0)$에서 턴을 맞이하는 사람은 항상 이긴다. 때문에 DP의 초기값은 다음과 같다:

$$D_{(0, 0, 0)} = \text{true}$$

이러한 DP를 naive 하게 구현하면 시간 복잡도는 $O(N^4)$이 되고, 이 시간 복잡도로도 100점을 받을 수 있다. DP의 시간 복잡도를 좀 더 개선하면 $O(N^3)$도 가능하다.

더보기

12. 사회적 거리두기

$N \times N$ 격자 판이 있다. 이 격자 판에서 격자 칸 일부를 선택하는데, 상하좌우 4방향과 대각선 4방향, 총 8방향에 인접하지 않도록 최대한 많은 칸을 선택하는 문제다. 단, 일부 칸은 선택할 수 없다.

 

이 문제는 실행 결과 제출형(Output only) 문제다. 그리고 문제 해결을 돕는 시뮬레이터가 제공되어 앞의 미션들은 손으로 해결하기 쉽다. 이 문제를 소스코드 작성으로 풀 경우 다음과 같은 풀이로 해결할 수 있다.

 

이 문제는 bitmask를 상태에 포함하는 bit DP로 해결할 수 있다. 아래와 같이 DP 배열 $D$를 정의하자.

$$D_{i, j, bitmask} = (i, j)\text{ 칸까지 선택 여부를 결정했고 최근 선택한 칸의 선택 여부가 }bitmask\text{일 때, 선택한 칸 수의 최댓값}$$

$bitmask$에 선택 여부가 포함되는 칸들

$(i, j)$ 칸을 $i$행 $j$열 칸이라고 하자. $(1, 1)$ 칸에서부터 오른쪽으로 차례대로 칸 선택 여부를 결정한다. 위 그림에서 $(i, j)$ 칸을 X가 적힌 칸이라고 했을 때, 빨간색 색칠된 칸에서 칸의 선택 여부를 $bitmask$에서 가지고 있는다. 그러면 $(i, j)$ 칸을 선택할 수 있는지 없는지 매 순간 판단할 수 있다. 만약에 칸을 선택할 수 있으면, 칸을 선택한 경우와 선택하지 않은 경우에 대해 DP 값을 뿌려주고, 칸을 선택할 수 없으면, 칸을 선택하지 않은 경우에 대해 DP 값을 뿌려주면 된다.

더보기

13. 물풍선 아티스트

매우 거대한 격자 판에서 일부 격자 칸이 색칠되어 있다. 물풍선을 터뜨려 칸을 색칠할 수 있는데, $(x, y)$칸에 세기 $p$인 물풍선을 놓아 터뜨리면 $(x-p, y), (x-p+1, y), \cdots, (x+p, y)$와 $(x, y-p), (x, y-p+1), \cdots, (x, y+p)$ 칸이 색칠된다. 물풍선의 세기 $p$는 0보다 크다. 색칠되어 있는 칸이 주어졌을 때, 어떻게 물풍선을 놓아 터뜨리면 되는지 구하는 문제다.

 

이 문제의 풀이는 간단하다. 세기가 1 이상인 물풍선을 놓을 수 있는 칸이 있으면 그 칸에 놓을 수 있는 가장 세기가 큰 물풍선을 놓는다. 그렇게 놓을 수 있는 물풍선을 전부 터뜨리고 색칠된 칸이 입력으로 주어진 칸과 같은지 확인하면 된다. 단, 구현을 $O(N \lg N)$ 시간 복잡도로 해야 한다. 입력으로 주어진 색칠된 격자 칸들을 좌표 순서대로 정렬한 뒤, 선형 시간에 작업하는 걸 반복하는 것으로 구현할 수 있다. 구현에 대한 자세한 설명은 생략한다. 아래 첨부된 코드를 참고하자.

더보기

14. 공격 상황 시뮬레이션

$x$축 위에 서로 다른 두 개의 점 $A$와 $B$가 주어진다. 그리고 서로 다른 $N$ 개의 점 $p_i$가 주어진다. 이때, 세 점 $A$, $B$, $p_i$로 그리는 삼각형 안에 점 $p_j$가 없는 $p_i$의 개수를 구하는 문제다. 단, 세 점 $A$, $p_i$, $p_j$가 일직선 상에 있는 경우가 없고, 세 점 $B$, $p_i$, $p_j$가 일직선 상에 있는 경우가 없으며 모든 점의 $y$ 좌표는 0보다 크다. ($i \ne j$)

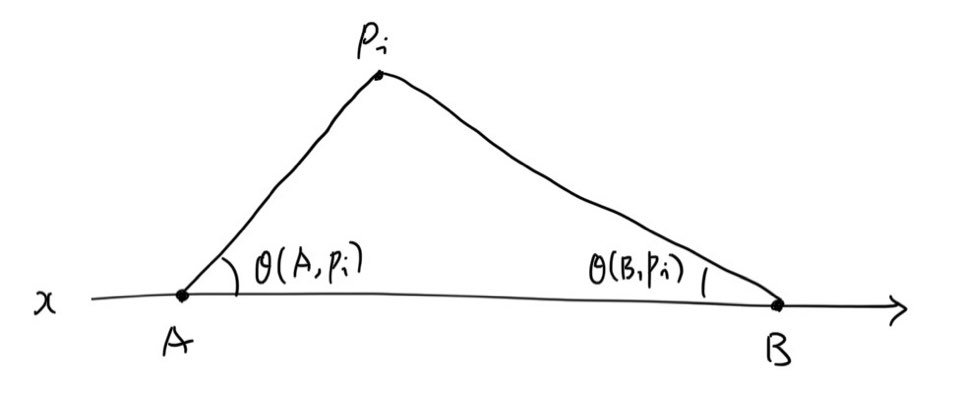
선분 $\overline{Ap_i}$와 선분 $\overline{A(\infty, 0)}$ 사이의 각도 $\theta(A, p_i)$ 순으로 점 $p_i$를 정렬했을 때, $p_i$가 있는 순서를 $a_i$라고 하자. 마찬가지로, 선분 $\overline{Bp_i}$와 선분 $\overline{B(-\infty, 0)}$ 사이의 각도 $\theta(B, p_i)$ 순으로 점 $p_i$를 정렬했을 때, $p_i$가 있는 순서를 $b_i$라고 하자. 이때, 세 점 $A$, $B$, $p_i$로 그리는 삼각형 안에 점 $p_j$가 있기 위한 필요충분조건은 $a_j \lt a_i$, $b_j \lt b_i$이다. 이를 이용하여 문제를 $O(N \lg N)$ 시간 복잡도로 해결할 수 있다. 단, 구현할 때 atan2 함수처럼 각도를 double로 표현해서 구해 정렬하지 말고, ccw를 이용하여 점을 각도 순으로 정렬하자.

더보기

15. 메이플 월드 라이딩 여행

$N$ 개의 정점과 $M$ 개의 간선으로 이루어진 방향성 그래프가 있다. 각 간선에는 길이가 매겨져  있다. 정점 $S$에서 시작하는 단순 경로들을 길이 순서로 정렬했을 때 $K$ 번째로 오는 경로의 길이를 구하는 문제다.

 

길이가 $x$ 이하인 단순 경로의 개수가 $K$ 개 이상인지 확인하는 결정 문제를 해결하여 Parametric Search로 이 문제를 해결할 수 있다. 우선 100점 풀이를 설명하기 전에 결정 문제를 $O(K^2)$ 시간 복잡도로 해결하는 54점 풀이를 먼저 설명하겠다. 우선, 정점의 인접 리스트를 간선 길이 순서로 정렬한다. 그리고 아래 코드처럼 DFS를 이용해 길이가 $x$ 이하인 단순 경로의 개수를 세면 시간 복잡도가 $O(K^2)$이 된다.

더보기

 

경로의 길이가 $x$를 넘어가게 되면 인접 리스트 순회를 멈추고, 찾은 단순 경로의 개수가 $K$ 이상이 되면 탐색을 멈추기 때문에 시간 복잡도가 $O(K^2)$가 된다. 이보다 더 시간 복잡도를 줄이기 위해서는 인접 리스트 순회 도중 방문한 정점을 처리하는 연산 횟수(위 코드에서 44번 줄의 continue 하는 횟수)를 줄여야 한다.

 

정점과 연결된 나가는 간선의 개수(out degree)가 $\sqrt{M}$ 이상인 정점을 거대한 정점이라고 부르자. 거대한 정점은 최대 $\sqrt{M}$ 개 있을 수 있다. 거대하지 않은 정점에 대해서는 기존과 같은 방법으로 인접 리스트를 순회하고, 거대한 정점에 대해서는 인접 리스트를 이중 연결 리스트(Doubly linked list)로 만들어서 관리하자. 어떤 정점이 방문되면 거대한 정점에서 방문한 정점으로 들어오는 간선에 대한 정보를 인접 리스트에서 제거한다. 마찬가지로, 어떤 정점의 방문이 해제되면 제거했던 정보를 다시 복원한다. 제거하고 복원하는 작업은 인접 리스트를 이중 연결 리스트로 만들었기 때문에 $O(1)$ 시간 복잡도에 된다. 정점이 방문되는 총 횟수는 최대 $K$고 한번 정점이 방문될 때마다 최대 $\sqrt{M}$ 번의 제거/복원 작업이 있으므로, 제거/복원 작업의 총 시간 복잡도는 $O(K\sqrt{M})$이 된다. 이처럼 방문된 정점을 인접 리스트에서 제거해주었기 때문에 거대한 정점에 대해 인접 리스트를 순회하는 총 시간 복잡도는 $O(K)$이다. 거대하지 않은 정점에 대해 인접 리스트를 순회하는 시간 복잡도는 정점당 $O(\sqrt{M})$이고 총 시간 복잡도는 $O(K\sqrt{M})$이다. 이런 방식으로 결정 문제를 해결할 때 시간 복잡도는 $O(N+M+K\sqrt{M})$이 된다.

 

Parametric search의 탐색 범위(정답으로 가능한 범위)를 $X$라고 할 때, 이 문제를 해결하는 풀이의 시간 복잡도는 $O((N+M+K\sqrt{M}) \lg X)$가 된다.

더보기

16. 덕분에 챌린지

$N+M$ 명의 사람이 덕분에 챌린지를 진행한다. 이들 중 한 명이 챌린지를 시작하여 진행하고, 다음으로 참여할 사람을 두 명 이하로 지목하여 지목받은 사람이 챌린지를 이어 나가는 방식으로 진행된다. 한 사람이 여러 번, 혹은 동시에 지목 당할 수 없다. 각 사람은 챌린지를 시작하여 완료하기까지 걸리는 시간이 정해져 있다. $N$ 명의 사람은 챌린지를 진행하는 시간이 $X$이고, $M$ 명의 사람은 챌린지를 진행하는 시간이 $Y$이다. 모든 사람이 챌린지를 마치는데 걸리는 최소 시간을 구하는 문제다.

 

일반성을 잃지 않고 $X \leq Y$라 하자. 다음과 같은 DP 배열 $D$를 정의할 수 있다.

$$D_{i,j} = \text{시간 }X\text{가 걸리는 사람 }i\text{ 명, 시간 }Y\text{가 걸리는 사람 }j\text{명이 챌린지를 마치는데 걸리는 최소 시간}$$

초기값은 $D_{0,0} = 0$이고, 정답은 $D_{N,M}$이 된다. $D$ 배열의 점화식은 다음과 같다:

$$D_{0,j} = D_{0,\lfloor\frac{j}{2}\rfloor} + Y\ (\forall j \geq 1)\\D_{i,j} = \min_{0 \leq k \lt i, 0 \leq l \leq j}\bigl(X+\max\left(D[k][l], D[i-k-1][j-l]\right)\bigr)\ (\forall i \geq 1, j \geq 0)$$

이 DP를 naive하게 구현하면 시간 복잡도 $O(N^2M^2)$이 되며 49점을 받을 수 있다.

 

$i$를 고정했을 때 $0 \leq j \leq M$인 $j$에 대해 모든 $D_{i, j}$를 빠르게 구하는 방법을 생각할 수 있다. 이 값을 구하기 위해 $k$를 고정하면, $D_k$와 $D_{i-k-1}$ 모두 감소하지 않는 배열임을 알 수 있다. 이 점을 이용하여 two pointers algorithm을 통해 $O(M)$ 시간에 특정 $k$에 대해 $D_i$ 배열에 최소 갱신을 해줄 수 있다. 이렇게 DP를 구현하면 시간 복잡도 $O(N^2M)$에 해결할 수 있다.

더보기

17. 좋은 카트 만들기

종류 1의 순서쌍 $(A_i, B_i)$가 $N$ 개 있고, 종류 2의 순서쌍 $(C_j, D_j)$가 $M$ 개 있다. 종류 1의 모든 순서쌍에 대해 $\frac{A_i+C_j}{B_i+D_j}$가 최대가 되는 $j$를 구하는 문제다. 만약, 가능한 $j$가 여러 가지인 경우 그중 가장 작은 $j$를 구하면 된다.

 

종류 2인 순서쌍 $(C_j, D_j)$에 대해 2차원 좌표 평면에 $(C_j, D_j)$ 좌표에 점을 그리자. 즉, 2차원 좌표 평면의 제1사분면에 점이 $M$개 그린다. 임의의 순서쌍 $(A_i, B_i)$에 대해 $\frac{A_i+C_j}{B_i+D_j}$가 최대가 된다는 것은 제3사분면의 점 $(-A_i, -B_i)$와 제1사분면의 $N$ 개의 점 중 하나를 골라 직선을 그렸을 때 그 직선의 기울기가 최대가 된다는 것이다. 즉, 제3사분면에 있는 점 $N$ 개에 대해 제1사분면에 있는 점 $M$ 개 중 한 점을 골라 직선을 그렸을 때 직선의 기울기가 최대가 되는 점을 찾는 문제로 바뀐다.

 

제1사분면에 있는 점 $N$ 개에 대해 Convex hull을 구했을 때, Convex hull 내부에 있는 점은 제3사분면에 있는 임의의 점과 직선을 그렸을 때 기울기가 최대가 될 수 없다. Convex hull을 구함으로 기울기가 최대가 되는 점의 후보를 줄일 수 있다. 좀 더 엄밀히 말하면, 기울기를 계산하는 다른 점이 항상 제3사분면에 있으므로 Convex hull 전체를 후보로 둘 필요 없이 Convex hull의 윗 부분만 가지고 있어도 된다. Convex hull의 윗 부분이 있을 때 제3사분면에 있는 임의의 점 $p$와 직선을 그렸을 때 기울기가 최대가 되는 점을 구하면 되는데, Convex hull의 윗 부분에 속하는 선분을 $\overline{a_ia_{i+1}}$라고 할 때, $\mathrm{ccw}(p, a_i, a_{i+1})$에 경향성이 있으므로 이분 탐색을 통해 $O(\lg N)$ 시간 복잡도에 구할 수 있다. 이 문제에서 큰 허들로 작용하는 것은 기울기가 같으면 그중 가장 작은 번호 $j$를 구하는 부분이다. Convex hull의 각 선분 마다 선분 안에 있는 점의 번호 중 가장 작은 값을 미리 전처리로 계산해두어 해결할 수 있다. 이 문제를 해결하는 총 시간 복잡도는 $O((N+M) \lg M)$이다.

더보기

18. 유저 그룹 나누기

배열 $U$가 주어졌을 때, 이 배열에 $K$ 개의 파티션을 만들어서, 파티션에 있는 원소 합의 최댓값과 최솟값의 차이를 최소화하는 문제다. 단, 입력으로 주어지는 $X$에 대해 $X \leq U_i \leq 2X$를 만족한다.

 

파티션에 있는 원소 합의 최솟값을 정해보자. 직관적으로 생각했을 때, 가능한 최솟값의 수는 $O(N^2)$이다. 정해진 원소 합의 최솟값 $x$에 대해, 다음과 같은 DP로 $K$ 개의 파티션을 만들었을 때, 파티션에 있는 원소 합의 최댓값을 최소화할 수 있다.

$$D_{i,j} = \text{1번 원소부터 }j\text{번 원소까지 부분 배열에서 }i\text{ 개의 파티션을 나누었을 때, 원소 합 최댓값의 최소값}$$

$$D_{i,j} = \min_{k \lt j,\ S_j-S_k \geq x}\bigl(\max\left(D_{i-1,k}, S_j-S_k\right)\bigr)$$

위와 같은 DP 배열은 naive하게 $O(KN^2)$ 시간 복잡도로 해결할 수 있으며, 이렇게 해결할 경우 총 시간 복잡도는 $O(N^4K)$가 되고 8점을 받을 수 있다.

 

파티션 $K$ 개를 만들기 위해서는 자명하게 $\frac{\sum U_i}{K}$ 이하인 최솟값에 대해서만 고려하면 된다. 이보다 큰 값을 합의 최솟값으로 결정할 경우 만들 수 있는 파티션의 수는 $K$ 보다 작아진다. 이 문제에는 $X \leq U_i \leq 2X$라는 특이한 조건이 있다. $\sum U_i \leq 2XN$이며, 이로 인해 가능한 최솟값의 후보 개수를 $O\bigl(\frac{N^2}{K}\bigr)$로 줄이는 것이 가능하다. 이렇게 줄이면 총 시간 복잡도는 $O(N^4)$이 되며, 31점을 받을 수 있다.

 

100점을 받기 위해서는 Divide & Conquer Optimization이 필요하다. $D_{i, j}$가 되는 가장 작은 $k$ 값을 $K_{i, j}$라고 정의하자. 위와 같은 점화식 꼴에서 $K_{i, j} \leq K_{i, j+1}$가 만족되면 Divide & Conquer Optimization이 가능하다. 이와 같은 사실은 DP 정의를 보면 맞을 것 같다는 생각이 들고, 증명 가능하다. 증명에 대해서는 이 글에서 다루지 않겠다. Divide & Conquer Optimization을 통해 총 시간 복잡도를 $O(N^3 \lg N)$으로 줄일 수 있다.

더보기

19. 서비스 센터

$x$축 위에 서비스 센터 $N$ 개가 주어진다. $i$ 번째 서비스 센터의 위치는 $(x_i, 0)$이며, 맨허튼 거리로 $L_i$ 이하인 사무실에 방문하여 서비스를 제공할 수 있다. $M$ 개의 사무실이 있다. $i$ 번째 사무실의 위치는 $(p_i, q_i)$이며, 총 $C_i$ 번의 방문 서비스가 필요하다. 서비스 센터에서 방문 서비스를 한 번 진행하는데 1일이 소요된다. 모든 사무실에 원하는 만큼 방문 서비스를 해줄 때 필요한 소요 시간의 최솟값을 구하는 문제다.

 

서비스 센터마다 방문 서비스를 $x$ 번 이하로 할 때, 모든 사무실에 원하는 만큼 방문 서비스를 제공할 수 있는지 확인하는 결정 문제를 해결하여 Parametric Search로 이 문제를 해결할 수 있다. 우선 맨허튼 거리 제한 $L_i$가 서비스 센터마다 주어지는데, $(x, y)$ 좌표를 $(x-y, x+y)$로 바꿔 서비스 센터가 방문 가능한 범위를 좌표 축에 평행한 정사각형 영역으로 표현할 수 있다.

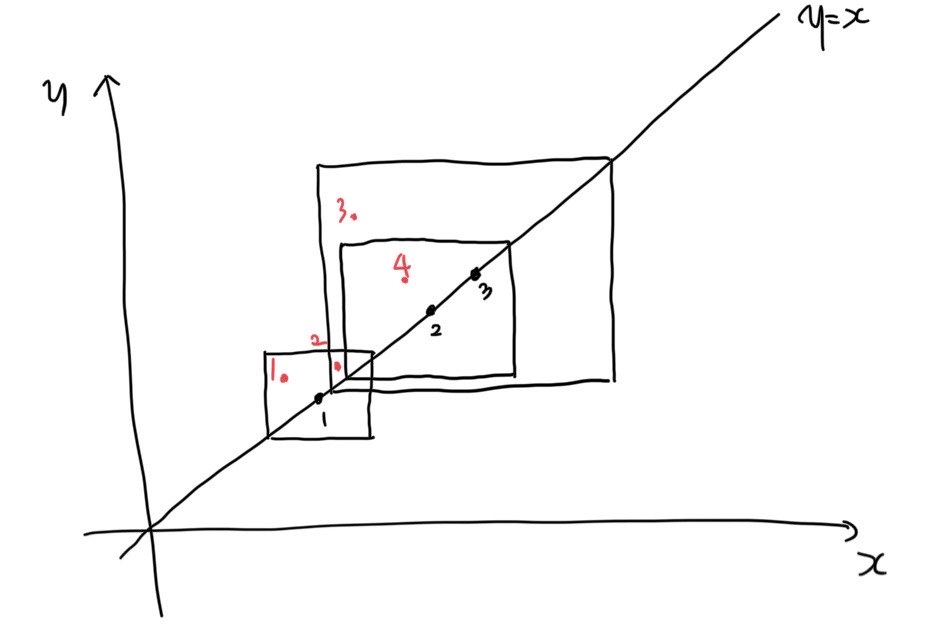
검은색 점이 서비스 센터의 위치고 검은 테두리 정사각형은 그 서비스 센터가 방문 가능한 범위를 표현한다. 빨간점은 사무실을 나타내며 $x$ 좌표 순으로 정렬하여 번호가 매겨져 있다. 일반성을 잃지 않고 빨간점이 $y=x$ 직선보다 아래 영역에 없다고 가정할 수 있다. (만약, $y=x$ 직선보다 아래 영역에 있으면 $y=x$ 직선 기준으로 선대칭 이동하면 된다.) 이렇게 매긴 번호 순서대로 사무실에 방문할 서비스 센터를 선택하는 작업을 한다. 방문 서비스할 서비스 센터를 선택할 때에 방문 가능한 서비스 센터 중에서 방문 가능한 범위의 $y$ 좌표 상한이 제일 작은 서비스 센터를 우선적으로 고르는 욕심쟁이 기법으로 결정 문제를 해결할 수 있다. 모든 서비스 센터의 위치가 $y=x$ 직선 위에 있고 모든 빨간점이 $y=x$ 직선보다 아래 영역에 있지 않으므로 set을 이용한 간단한 구현이 가능하다.

더보기

20. 물풍선 테러리스트

매우 거대한 격자 판의 일부 격자 칸 위에 물풍선이 놓여있다. $i$ 번째 물풍선의 위치는 $(x_i, y_i)$이고, 세기는 $p_i$이다. $i$ 번째 물풍선이 터지면 $(x_i-p_i, y_i), (x_i-p_i+1, y_i), \cdots, (x_i+p_i, y_i)$와 $(x_i, y_i-p_i), (x_i, y_i-p_i+1), \cdots, (x_i, y_i+p_i)$ 칸에 폭발이 닿으며 폭발이 닿은 칸에 물풍선이 있을 경우 그 물풍선도 터지는 연쇄적인 폭발이 일어난다. 원하는 물풍선에 바늘을 던저 터뜨리는 작업을 할 수 있다. 가장 적은 수의 바늘을 사용하여 모든 물풍선을 터뜨리는 경우 필요한 바늘의 수와, 가장 많은 수의 바늘을 사용하여 모든 물풍선을 터뜨리는 경우 필요한 바늘의 수를 구하는 문제다.

 

$i$ 번째 물풍선을 정점 $i$로 만들고, 이 물풍선이 터졌을 때 $j$ 번째 물풍선에 닿으면 정점 $i$에서 정점 $j$로 가는 방향성 간선을 만든다. 이렇게 만들어진 방향성 그래프에서 강한 연결 요소(Strongly Connected Component, SCC)를 구해서 그래프를 DAG로 만든다. DAG에서 in degree가 0인 정점의 수는 필요한 바늘의 최소 개수고, DAG에서 정점의 개수(즉, 강한 연결 요소의 개수)는 필요한 바늘의 최대 개수가 된다. 이걸 naive하게 구현하면 시간 복잡도는 $O(N^2)$이며, 21점을 획득한다.

 

위에서 설명한 방법에서 시간 복잡도가 $O(N^2)$까지 커지는 이유는 처음 만든 방향성 그래프에서 간선의 개수가 최대 $O(N^2)$ 개 있을 수 있기 때문이다. 이 문제의 100점 풀이로 접근하기 위해서는 만드는 간선의 수를 줄여야 한다.

 

어떤 물폭탄의 폭발 범위는 +자 모양으로 가로 선분과 세로 선분으로 분리해서 생각할 수 있다. 이 물폭탄이 폭발할 때 폭발 범위의 가로 선분에서 닿는 물폭탄의 번호는 물폭탄들이 $y$, $x$ 좌표 순으로 정렬되어 있을 때 연속하다. 즉, 연속한 범위에 있는 물폭탄들에게 나가는 간선을 연결해주는데 아래와 같은 방법으로 연결하는 간선 수를 줄일 수 있다.

예를 들어, 정점 $v$에서 정점 $3$부터 정점 $8$까지 연속한 6개의 정점에 나가는 간선을 연결한다고 하자. Naive하게 간선을 추가하면 6개의 간선을 추가하는데, 다음과 같이 세그먼트 트리를 구성할 때와 비슷하게 가상 정점과 가상 간선들(그림에서 파란색)을 만들어 준 후, 그 가상 정점을 향하는 2개의 간선(그림에서 빨간색)만 추가하면 6개 정점에 모두 나가는 간선을 만드는 것과 같은 상황이 된다. 즉, 크기가 $r$인 연속한 범위의 정점에 간선을 연결하는 상황이 간선을 $r$ 개 추가하는 것이 아닌, 최대 $2 \lg r$ 개 간선만 추가해도 된다. 세로 선분에서 닿는 물폭탄의 번호는 물폭탄들이 $x$, $y$ 좌표 순으로 정렬되어 있을 때 연속하기 때문에 마찬가지의 방법으로 간선을 만들 수 있다.

 

이렇게 간선을 만들 경우 간선의 수가 $O(N^2)$이 아닌 $O(N \lg N)$ 개가 된다. 다만, 사용하는 바늘 개수의 최솟값과 최댓값을 구할 때 가상 정점들로만 이루어진 SCC를 고려하지 않는 등의 후처리가 필요하다. 이 풀이의 총 시간 복잡도는 $O(N \lg N)$이다.

더보기

'해법' 카테고리의 다른 글

Google Code Jam 2022 Round 2 풀이 및 후기  (0) 2022.05.16
Nexon Youth Programming Challenge(NYPC) 2021 예선 풀이  (3) 2021.08.28
Google CodeJam 2019 Round 2 풀이  (1) 2019.05.21
2018년 아시아태평양 정보올림피아드 (APIO2018) 풀이  (1) 2018.05.17
제34회 한국정보올림피아드 (KOI 2017) 중등부 풀이  (4) 2017.07.27
공유하기 링크
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
Total
Today
Yesterday
링크
TAG more
«   2024/04   »
일 월 화 수 목 금 토
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30
글 보관함