Nexon Youth Programming Challenge(NYPC) 2021 예선 풀이

티스토리 뷰

해법

Nexon Youth Programming Challenge(NYPC) 2021 예선 풀이

전명우 2021. 8. 28. 17:29

1. 계단

$1$ 층부터 $M$ 층까지 총 $M$ 개의 층이 있는 건물이 있다. 건물의 $F$ 층에서 시작하여 계단을 통해 한 층을 올라가거나, 엘리베이터를 타고 원하는 층으로 이동할 수 있다. 정확히 $N$ 번 계단을 통해 층을 오르면서 엘리베이터를 적절히 타서 $F$ 층으로 돌아오고 싶다. 이때, 엘리베이터를 타는 횟수의 최솟값을 구하는 문제다.

문제에서 $F$가 입력으로 주어지지만, $F$는 답에 영향을 미치지 않는다는 것을 알 수 있다. 답은 $\left\lceil\frac{N}{M-1}\right\rceil$이다.

2. 레이스 기록 검증

$N$ 명의 유저가 있고, 유저들의 레이스 시작 로그, 레이스 종료 로그가 발생 시간과 함께 주어진다. 주어지는 로그의 개수는 총 $M$ 개다. 정상적인 레이스는 1분이상 걸려처 유저가 59초 이내에 레이스를 종료한 적이 있으면 올바르지 않은 기록이다. 레이스를 시작하지 않은 유저가 레이스를 종료하거나, 레이스를 시작한 유저가 레이스를 종료하기 전에 다시 레이스를 시작하거나, 레이스를 시작한 유저가 레이스를 종료하지 않은 상태로 끝까지 있는 경우 또한 올바르지 않은 기록이다. 주어진 로그가 올바른지 아닌지 판단하는 문제다.

문제에서 말하는 대로 구현을 하는 문제다. 구현은 아래 첨부된 코드를 참고하자.

3. 근무표 짜기

$N$ 명의 직원이 있고, 출근해야 하는 날이 $K$ 개 있다. 각 날 별로 최대로 출근할 수 있는 인원 제한이 주어지고, 각 직원이 반드시 출근해야 하는 날 수가 주어진다. 이때, 각 날마다 출근하는 직원들을 적절히 정하여 주어진 조건을 모두 만족하는 근무표를 만드는 문제다.

각 날마다 직원들 중에 남아있는 근무 일수가 많은 사람들부터 출근시키는 그리디 방법이 올바른 근무표를 구한다. $N$, $K$의 최댓값이 100으로 작은 편이므로 $O(KN^2)$ 풀이도 만점을 받을 수 있다.

4. 파티

$N$ 명의 사람이 있다. $i$ 번 사람은 파티에 $M_i$ 만큼의 돈을 지불했다. 이들은 파티가 끝난 후, 돈을 적게 쓴 사람이 돈을 많이 쓴 사람에게 돈을 주는 방식으로 최대한 공평하게 더치페이를 하려고 한다. 돈은 소수점 자리를 가질 수 없으므로, 최대한 공평하다는 것은 최종적으로 각 사람마다 지불한 액수의 최댓값과 최솟값의 차이를 최소화한다는 의미다. 이때, 이동한 총 금액을 최소화하는 문제다.

문제의 각색이 살짝 복잡하게 되어 있는데, 결국 $N$ 명의 사람이 각각 돈을 $M_i$ 만큼 가지고 있는 상황에서 서로 돈을 적절히 옮겨, 가장 돈을 많이 가지고 있는 사람과 적게 가지고 있는 사람의 차이를 최소화하는 문제다. 이 차이의 최솟값은 $M_i$의 합이 $N$으로 나누어 떨어지면 0이고, 그렇지 않으면 1이다. $M_i$의 합을 $N$으로 나눈 나머지를 $K$라고 하자. 최종적으로 $K$ 명은 돈을 가장 적게 가지고 있는 사람보다 1원 더 많이 가지고 있을 것이고, $N-K$ 명은 가장 적은 액수를 가지고 있을 것이다. 이동한 총 금액을 최소화하기 위해서 처음에 돈을 많이 가지고 있는 상위 $K$ 명이 최종적으로 돈을 가장 적게 가지고 있는 사람보다 1원 더 많이 가지고 있으면 된다. 이는 단순한 정렬로 구현 가능하므로, 시간복잡도는 $O(N \lg N)$이 된다.

5. 페인트 칠하기

$N \times M$ 크기의 격자판이 있다. 처음에 각 격자칸은 흰색이고, 한 행이나 한 열에 특정 색을 덧칠하는 연산을 할 수 있다. 최종적으로 격자칸 마다 어떤 색이 칠해져야 하는지 주어진다. 덧칠하는 연산을 적절히 사용하여 각 격자칸을 주어진 색으로 칠하는 문제다.

이 문제는 실행 결과 제출형(Output only) 문제다. 그리고 문제 해결을 돕는 시뮬레이터가 제공되어 앞의 미션들을 손으로 해결할 수 있다.

이 문제를 소스 코드를 작성하여 풀 경우 다음과 같은 풀이로 해결할 수 있다. 가장 마지막에 칠해진 연산이 무엇인지 유추할 수 있다. 한 행이 전부 같은 색이거나, 한 열이 전부 같은 색이라면 그 행 혹은 그 열이 마지막으로 칠해졌다. 그러면 그 행 혹은 그 열에 있는 색을 무엇이든 가능한 색으로 바꾼다. 이 과정을 반복하면 결국 격자칸의 모든 칸은 무엇이든 가능한 색이 된다. 이 과정을 반대로 하면 처음에 입력으로 주어진 격자판을 만들 수 있다.

#include <bits/stdc++.h>
using namespace std;

int N, M;
int A[102][102];

int main()
{
    scanf("%d%d", &N, &M);
    for (int i=1;i<=N;i++) for (int j=1;j<=M;j++) scanf("%d", A[i]+j);
    vector<tuple<char, int, int>> ans;
    for (;;){
        bool is_end = 1;
        for (int i=1;i<=N;i++) for (int j=1;j<=M;j++) if (A[i][j]) is_end = 0;
        if (is_end) break;
        bool changed = 0;
        for (int i=1;i<=N;i++){
            int c = 0; bool imp = 0;
            for (int j=1;j<=M;j++) if (A[i][j]){
                if (c && c != A[i][j]) imp = 1;
                c = A[i][j];
            }
            if (!c || imp) continue;
            ans.emplace_back('H', i, c);
            for (int j=1;j<=M;j++) A[i][j] = 0;
            changed = 1;
        }
        for (int j=1;j<=M;j++){
            int c = 0; bool imp = 0;
            for (int i=1;i<=N;i++) if (A[i][j]){
                if (c && c != A[i][j]) imp = 1;
                c = A[i][j];
            }
            if (!c || imp) continue;
            ans.emplace_back('V', j, c);
            for (int i=1;i<=N;i++) A[i][j] = 0;
            changed = 1;
        }
        assert(changed);
    }
    reverse(ans.begin(), ans.end());
    printf("%d\n", ans.size());
    for (auto [d, t, c]: ans) printf("%c %d %d\n", d, t, c);
}

6. 폭탄 터트리기

$N$ 개의 폭탄이 있고, $i$ 번 폭탄에는 수 $A_i$가 적혀있다. 수 $X$가 적힌 폭탄을 클릭하면, 클릭한 폭탄을 포함하여 연속적으로 인접하면서 적힌 수가 $X$ 이상 $X+K$ 이하인 모든 폭탄이 같이 터진다. $N$ 개의 폭탄을 모두 터트리기 위해 필요한 클릭의 최소 횟수를 구하는 문제다.

이 문제는 남아있는 폭탄 중 적힌 수가 가장 작은 폭탄을 클릭하는 것을 반복하여 해결할 수 있다. 클릭한 폭탄과 연속적으로 인접하면서 적힌 수가 $X$ 이상 $X+K$ 이하인 폭탄을 반복문으로 매번 구하여도, 시간복잡도가 $O(N)$이 되어 문제를 간단히 해결할 수 있다. 다만, 처음에 폭탄들을 적힌 수에 따라 오름차순으로 정렬해야 하기 때문에 풀이의 전체 시간복잡도는 $O(N \lg N)$이 된다.

7. 루트가 많은 트리?

$N$ 개의 정짐이 있는 트리가 주어진다. 다만 트리의 각 간선은 방향이 없거나, 방향이 정해져 있다. 방향이 없는 간선들의 방향을 적절히 정해 트리를 루트가 있는 트리(rooted tree)로 만들 수 있는데, 이때 루트로 가능한 정점의 개수를 구하는 문제다.

주어진 트리에서 정점 $a$에서 정점 $b$로 가는 방향성 간선이 있다고 하자. 그러면 최종 트리에서 정점 $b$의 부모는 항상 정점 $a$가 된다. 또한, 정점 $b$와 연결된 다른 정점들은 정점 $b$의 자식 정점이 된다. 이 과정을 반복할 수 있다. 이런 방법으로 flood fill을 할 수 있다. Flood fill을 한 이후에도 부모 정점이 없는 정점들이 루트로 가능한 정점이다.

8. 영역 나누기

원주 위에 $2N$ 개의 점이 있다. 각 점에는 $1$ 이상 $N$ 이하의 번호가 적혀있으며, 같은 번호가 적힌 점은 정확히 2개 있다. 같은 번호가 적힌 두 개의 점을 연결하는 선분을 그어 원 안에 여러 영역이 생긴다. 점들의 순서가 바뀌지 않게 원주 위의 점들을 적절히 이동하여, 생기는 영역의 개수를 최대화 하는 문제다.

처음에 아무런 선분이 없이 원만 있을 때, 영역의 개수는 1개다. 이때, 선분을 하나씩 그려나가 선분을 그린 직후 영역의 개수가 몇개 증가하는지 알 수 있다. 선분을 그릴 때 교차한 선분의 개수+1개 만큼 영역의 개수는 증가한다. 예를 들어, 아래와 그림과 같이 선분을 그리는 경우를 생각해보자.

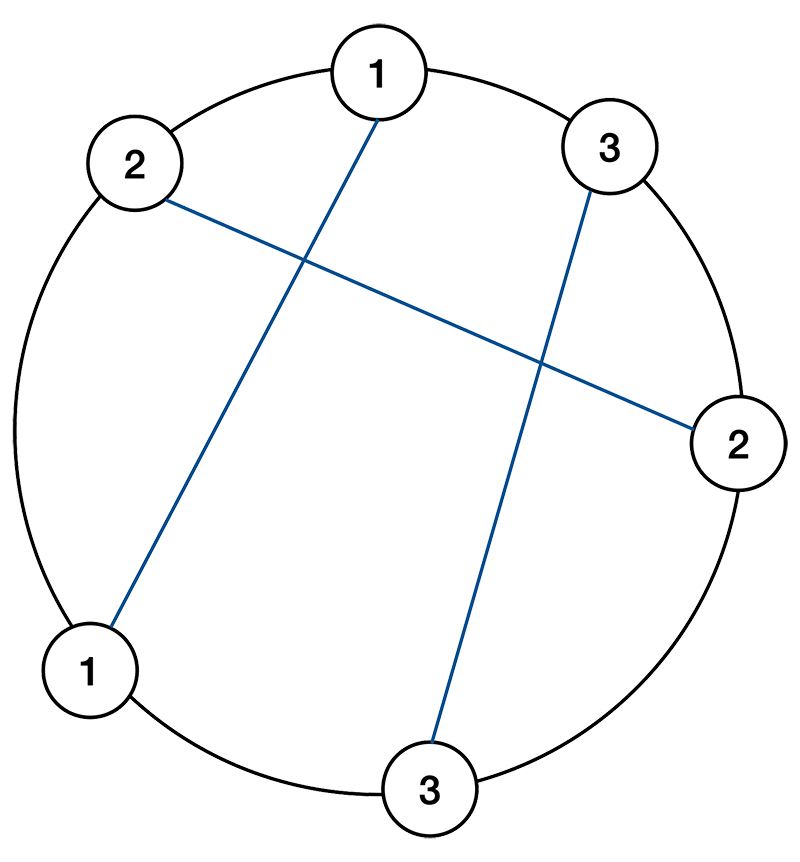
처음에 1번 정점을 연결하는 선분을 그릴 때는 교차하는 선분의 개수가 0이기 때문에, 영역의 개수가 1 증가하여, 영역의 개수는 2개가 된다. 두 번째로 2번 정점을 연결하는 선분을 그릴 때는 교차하는 선분의 개수가 1이기 때문에, 영역의 개수가 2 증가하여, 영역의 개수가 4개가 된다. 마지막으로 3번 정점을 연결하는 선분을 그릴 때는 교차하는 선분의 개수가 1이기 때문에, 영역의 개수가 2 증가하여, 영역의 개수가 6개가 된다. 이렇게 영역의 개수가 6개라는 것을 구했다.

100점을 받기 위해서는 $O(N \lg N)$ 시간복잡도로 이 알고리즘을 구현해야 하는데, 선분을 그리는 순서를 잘 정하고 BIT(Binary Indexed Tree, Fenwick Tree)를 이용하여 구현할 수 있다.

9. K-좀비

$N \times M$ 크기의 격자판이 있다. 우니는 $1$행$1$열에서 시작하여 $N$행$M$열까지 상하좌우로 이동해서 가려고 한다. 시각은 0에서부터 시작하여 우니가 한 칸 이동할 때마다 1이 증가한다. 격자칸에는 장애물이나 $K$-좀비가 있을 수 있다. 우니는 장애물과 $K$-좀비가 있는 칸에 갈 수 없고, 시각이 $K$의 배수가 아니면 $K$-좀비에 인접한 칸에도 갈 수 없다. 시각 $100\,000$ 이내에 도착지점까지 가는 이동 커맨드를 구하는 문제다.

이 문제는 실행 결과 제출형(Output only) 문제다. 그리고 문제 해결을 돕는 시뮬레이터가 제공되어 앞의 미션들을 손으로 해결할 수 있다. 다만, 뒤에 있는 미션일 수록 이동 커맨드의 최소 길이가 점점 커지기 때문에 손으로 해결하기 힘들다. 특히, 미션10의 경우 도착 지점으로 가는 이동 커맨드의 최소 길이가 정확히 $100\, 000$이므로, 손으로는 거의 불가능하다.

이 문제를 소스 코드를 작성하여 풀 경우 다음과 같은 풀이로 해결할 수 있다. 가능한 $K$의 범위가 $1$ 이상 $9$ 이하로 작다. $1$부터 $9$의 최소 공배수를 구하면 $2\,520$이다.

다음과 같은 DP 배열을 정의하자.

D[i][j][k] = i행j열의 격자칸에 시각 k(단, k는 시각을 2520으로 나눈 나머지)에 있을 경우, 오는데 걸리는 최소 시각(즉, 이동 커맨드의 최소 길이)

초기값은 D[1][1][0] = 0이며, 점화식은 상하좌우로 이동하고, 장애물과 $K$-좀비를 고려하여 적절하게 만들 수 있다. 이 DP는 BFS로 간단하게 구현할 수 있다. 시간복잡도는 $O(2520 \times NM)$이다.

#include <bits/stdc++.h>
using namespace std;

int yy[]={-1, 0, 1, 0}, xx[]={0, 1, 0, -1};
const string dch = "URDL";
const int MOD = 2520; // lcm from 1 to 9
int N, M;
char A[26][27];
int D[26][26][MOD], E[26][26][MOD];

bool available(int y, int x, int t)
{
    for (int i=0;i<4;i++){
        int ny = y+yy[i], nx = x+xx[i];
        if (ny < 1 || ny > N || nx < 1 || nx > M || !isdigit(A[ny][nx])) continue;
        int c = A[ny][nx]-'0';
        if (t % c != 0) return 0;
    }
    return 1;
}

int main()
{
    scanf("%d%d", &N, &M);
    for (int i=1;i<=N;i++) scanf("%s", A[i]+1);
    for (int i=1;i<=N;i++) for (int j=1;j<=M;j++) for (int k=0;k<MOD;k++) D[i][j][k] = -1;

queue<tuple<int, int, int>> que;
    D[1][1][0] = 0; que.push({1, 1, 0});
    while (!que.empty()){
        auto [y, x, md] = que.front(); que.pop();
        for (int dir=0;dir<4;dir++){
            int ny = y+yy[dir], nx = x+xx[dir], nmd = (md+1)%MOD;
            if (ny < 1 || ny > N || nx < 1 || nx > M || A[ny][nx] != '.' || D[ny][nx][nmd] != -1) continue;
            if (!available(ny, nx, nmd)) continue;
            D[ny][nx][nmd] = D[y][x][md]+1;
            E[ny][nx][nmd] = dir;
            que.push({ny, nx, nmd});
        }
    }
    int ans = 2e9, y = N, x = M, md;
    for (int i=0;i<MOD;i++) if (D[N][M][i] != -1 && ans > D[N][M][i]){
        ans = D[N][M][i]; md = i;
    }
    string path;
    while (D[y][x][md] > 0){
        int from = E[y][x][md];
        y -= yy[from], x -= xx[from];
        path.push_back(dch[from]);
        md = (md-1+MOD)%MOD;
    }
    reverse(path.begin(), path.end());
    puts(path.c_str());
}

10. 다양성이 힘이다

양의 정수 $N$ 개로 이루어진 배열이 있다. 이 배열에서 크기가 $K$인 부분 배열을 찾아 다양성 값을 구할 것이다. 다양성 값은 부분 배열에 속한 임의의 두 원소 값의 차이의 합이다. 이런 다양성 값의 최댓값을 구하는 문제다.

맨 처음에 배열의 첫 $K$개 원소로 이루어진 부분 배열에 대해 다양성 값을 구하고, 이후에는 부분 배열의 맨 오른쪽에 원소를 추가하고, 부분 배열의 맨 왼쪽에서 원소를 제거하는 방식으로 모든 부분 배열에 대해 다양성 값을 구한다. 이루어진 부분 배열에 원소를 추가하고, 원소를 제거하면서 다양성 값의 변화를 잘 구해야 하는데, 이는 어떤 원소보다 큰 원소의 개수와 그 원소들의 합을 BIT(Binary Indexed Tree, Fenwick Tree)를 이용해서 구할 수 있다. 시간복잡도는 $O(N \lg N)$이다.

#include <bits/stdc++.h>
using namespace std;

#define MAXN 200005
typedef long long lld;

int N, K;
int A[MAXN], B[MAXN];

template <typename T = int>
struct BIT{
    int n;
    vector<T> tree;
    BIT(int n): n(n), tree(n+1) {}
    void add(int x, T v){ for (;x<=n;x+=x&-x) tree[x] += v; }
    T get(int x){
        T ret = 0;
        for (;x;x^=x&-x) ret += tree[x];
        return ret;
    }
};

int main()
{
    scanf("%d%d", &N, &K);
    for (int i=1;i<=N;i++) scanf("%d", A+i);

vector<int> num;
    for (int i=1;i<=N;i++) num.push_back(A[i]);
    sort(num.begin(), num.end());
    for (int i=1;i<=N;i++) B[i] = lower_bound(num.begin(), num.end(), A[i])-num.begin()+1;

BIT cnt(N);
    BIT<lld> sum(N);
    lld now = 0;
    auto apply = [&](int x, int v, int sign = 1){
        {
            int c = cnt.get(N)-cnt.get(x);
            lld s = sum.get(N)-sum.get(x);
            now += (s-(lld)c*v)*sign;
        }
        {
            int c = cnt.get(x-1);
            lld s = sum.get(x-1);
            now += ((lld)c*v-s)*sign;
        }
        cnt.add(x, 1*sign);
        sum.add(x, v*sign);
    };
    lld ans = 0;
    for (int i=1;i<=N;i++){
        apply(B[i], A[i]);
        if (i-K > 0) apply(B[i-K], A[i-K], -1);
        if (i >= K) ans = max(ans, now);
    }
    printf("%lld\n", ans);
}

11. 원룸 구하기

1차원 좌표 공간에 $N$ 개의 가게가 있다. 각 가게는 $1$부터 $K$까지 $K$ 개 종류 중 하나다. 위치 $x$에 원룸을 짓는다는 쿼리가 $M$ 개 주어진다. 각 쿼리마다 주어진 원룸과 $K$ 개 종류에서 각 종류마다 적어도 1개의 가게를 포함하는 구간의 최소 크기를 구하는 문제다.

$K$ 개 종류에서 종류마다 적어도 1개의 가게를 포함하는 minimal 구간들을 구할 수 있다. 쿼리에서 정답이 되는 구간은 주어진 원룸 위치 $x$에 이 minimal 구간 중 하나를 가져다 붙인 꼴이다. 즉, 위치 $x$를 포함하는 minimal 구간이 있다면, 그 minimal 구간 중 가장 작은 크기의 구간이 쿼리의 답이 된다. 만약, 위치 $x$를 포함하는 minimal 구간이 없다면, 위치 $x$보다 왼쪽에 있으면서 가장 오른쪽에 있는 minimal 구간에 $x$를 이어 붙이거나, 위치 $x$보다 오른쪽에 있으면서 가장 왼쪽에 있는 minimal 구간에 $x$를 이어 붙인 것이 쿼리의 답이 된다. 이 minimal 구간들을 시작점 기준으로 오름차순 정렬할 경우, 끝 점 또한 감소하지 않는다는 사실을 이용하여 deque로 전체 시간복잡도 $O(N \lg N + Q \lg Q)$에 문제를 해결할 수 있다.

#include <bits/stdc++.h>
using namespace std;

#define MAXN 500005

int N, K, Q;

struct Z{
    int p, t;
} A[MAXN];

struct Query{
    int x, idx;
} queries[MAXN]; int ans[MAXN];

int main()
{
    scanf("%d%d%d", &N, &K, &Q);
    for (int i=1;i<=N;i++) scanf("%d%d", &A[i].p, &A[i].t);
    sort(A+1, A+N+1, [](const Z &a, const Z &b){
        return a.p < b.p;
    });
    for (int i=1;i<=Q;i++){
        scanf("%d", &queries[i].x);
        queries[i].idx = i;
        ans[i] = numeric_limits<int>::max();
    }
    sort(queries+1, queries+Q+1, [](const Query &a, const Query &b){
        return a.x < b.x;
    });

vector<pair<int, int>> segs;
    int kinds = 0;
    vector<int> cnt(K+1);
    for (int i=1,j=1;i<=N;i++){
        while (j <= N && kinds < K){
            if (!cnt[A[j].t]++) kinds++;
            j++;
        }
        if (kinds == K)
            segs.emplace_back(A[i].p, A[j-1].p);
        if (!--cnt[A[i].t]) kinds--;
    }

deque<pair<int, int>> dq;
    int left = numeric_limits<int>::min();
    for (int i=1,j=0;i<=Q;i++){
        auto [x, idx] = queries[i];
        while (j < segs.size() && segs[j].first <= x){
            int sz = segs[j].second-segs[j].first;
            while (!dq.empty() && dq.back().second-dq.back().first >= sz) dq.pop_back();
            dq.emplace_back(segs[j]);
            j++;
        }
        while (!dq.empty() && dq.front().second < x){
            left = max(left, dq.front().first);
            dq.pop_front();
        }
        if (left > numeric_limits<int>::min()) ans[idx] = min(ans[idx], x-left);
        if (j < segs.size()) ans[idx] = min(ans[idx], segs[j].second-x);
        if (!dq.empty()) ans[idx] = min(ans[idx], dq.front().second-dq.front().first);
    }

for (int i=1;i<=Q;i++) printf("%d\n", ans[i]);
}

12. 생존 신호

$H \times W$ 크기의 격자판의 테두리에 구멍이 뚫려있다. 격자칸의 일부에는 거울이 이미 놓여있거나, 거울을 임의로 놓을 수 있다. 거울은 수직, 수평, 혹은 대각선 2방향 중 하나로 놓을 수 있다. 뚫려진 구멍을 통해 생존 신호를 쏴서 주어진 조건을 만족하게 생존 신호가 이동하여야 한다. 생존 신호의 이동 거리를 생존 신호의 세기라고 할 때, 이 세기를 최대화 시키는 문제다.

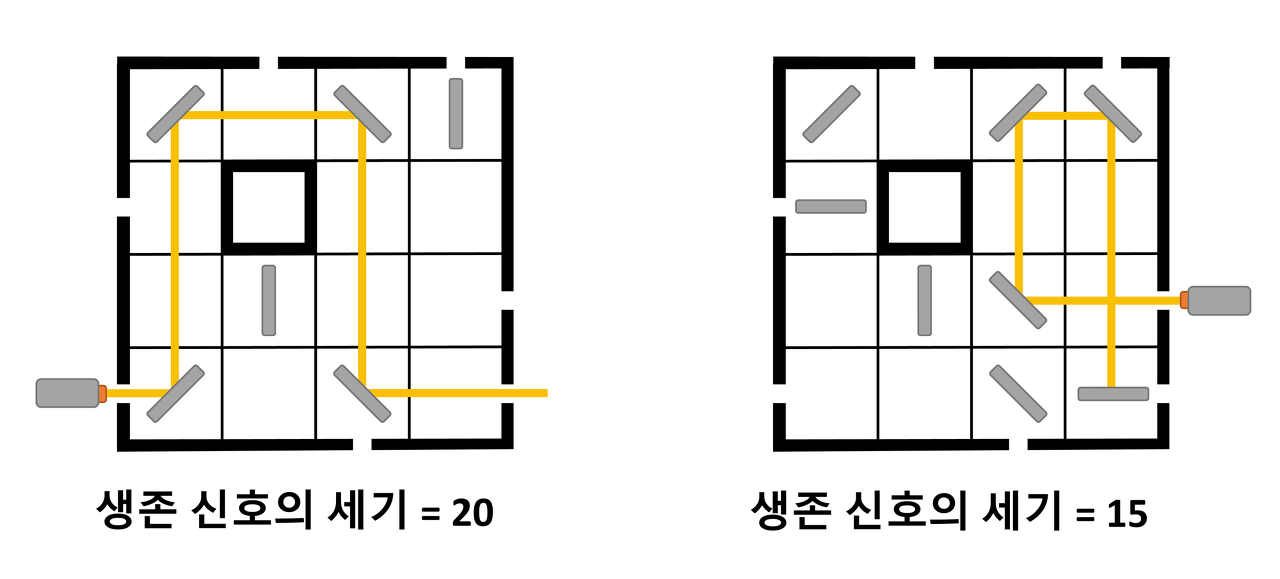
이 문제는 실행 결과 제출형(Output only) 문제다. 그리고 문제 해결을 돕는 시뮬레이터가 제공되어 앞의 미션들을 손으로 해결할 수 있다.

이 문제는 만들어내는 생존 신호의 세기에 따라 부분 점수를 주기 때문에 최적화 문제로 보이지만, 사실 최적해를 빠른 시간 안에 구하는 풀이가 존재한다. (풀이 준비 중)

13. 선물 상자

$N$ 명의 어린이가 원형으로 둘러앉아 있고, $i$ 번 어린이는 $D_i$개의 사탕을 받을 수 있는 봉투를 가지고 있다. 시계 방향으로 돌아가면서 한 사람씩 지목한다. $M$ 번째로 지목된 어린이에게 사탕을 하나씩 주고, 이를 반복한다. 어떤 어린이가 사탕을 받고, 가지고 있는 봉투에 사탕이 가득 차면, 원에서 빠진다. 가장 마지막까지 원에 남아있는 어린이의 번호를 구하는 문제다.

이 문제는 Josephus Problem의 변형이다. 만약 $D_i$가 모두 $1$이라고 하면, 문제는 Josephus Problem이 된다. 문제에서 $D_i$ 제한과 $M$ 제한은 $1\,000\,000\,000$으로 상당히 크지만, $N$ 제한은 $2\,000$으로 작은 편이다. 주어진 $N$ 제한을 통해 $O(N^2)$ 시간복잡도의 풀이를 예상할 수 있는데, 매 순간마다 다음으로 나가게 될 어린이의 번호를 $O(N)$ 시간복잡도로 구하면 문제를 해결할 수 있다.

현재 상황에서 남아있는 어린이의 수를 $n$이라고 하자. $M$ 번째로 지목된 어린이의 번호를 수열로 나타낼 때, $\gcd(n, M)$의 주기를 가지고 반복하는 수열이 된다. 즉, 수열의 앞 $\gcd(n, M)$ 개의 어린이의 번호를 구하고, 그 어린이들 중 사탕 봉투에 남은 용량이 가장 적으면서 가장 수열의 앞에 나타나는 어린이가 원에서 나갈 어린이가 된다. 이런 방식으로 남아있는 어린이의 사탕 봉투에 남은 용량도 갱신할 수 있다. 이 과정을 반복하면 $O(N^2)$ 시간복잡도에 문제를 해결할 수 있다.

14. 파스칼 삼각형

파스칼 삼각형이 무한한 크기로 있다. 이 삼각형에서 역삼각형이 아닌 정삼각형 모양의 영역 안에 들어있는 수의 합이 $K$가 되는 정삼각형 영역의 수를 구하는 문제다. 예를 들어, $K=1$인 경우 정삼각형 영역의 수는 무한이며, $K=4$인 경우 정삼각형 영역의 수는 4개다.

이 문제는 테스트케이스의 수 $T$의 제한이 $4\,000$으로 크고, $K$의 제한이 $10^{18}$로 크다. $T$ 제한과 서브태스크 중 하나가 $K \le 10^{12}$임을 미루어 볼 때, 만점을 받기 위해서 최적화가 많이 필요하다는 것을 짐작할 수 있다.

풀이의 기본적인 아이디어는 $K$의 제한이 아무리 커도 64비트 정수형 표현 범위 안에 들어가며, 정삼각형 영역 안에 들어있는 수의 합이 $K$ 이하가 되기 위해서는 정삼각형의 크기가 60보다 크지 않다는 것이다. 그리고 $n$이 적당히 크다고 할 때, $r$이 조금만 커도 $n \choose r$의 값이 $K$의 범위를 초과한다는 것이다.

크기가 1인 정삼각형 영역에서 수의 합이 $K$가 되는 경우의 수를 구하는 방법을 알아보자. $K=1$인 경우는 조건을 만족하는 정삼각형의 개수가 무한이므로, 제외하고 생각하자. $r$ 값이 정해졌을 때, ${n \choose r} = K$와 $2r \le n$를 만족하는 $n$은 최대 1개다. 이 $n$을 이분탐색을 통해 구할 수 있다. 또한, $2r \le n$이라는 조건 때문에 ${n \choose r} = K$를 만족하는 $n$이 존재하기 위한 $r$의 범위는 $r \le 31$이다. 즉 정해진 $r$에 대해 조건을 만족하는 $n$이 존재하는지 확인하기 위한 이분탐색을 최대 31번 하면 크기가 1인 정삼각형의 개수를 셀 수 있다.

마찬가지의 방법으로, 정삼각형의 크기와 윗 꼭지점의 $r$을 정하고 이분탐색을 통해 조건을 만족하는 $n$ 값을 구할 수 있다. 다만, 정삼각형 영역에서 안에 있는 수의 합을 일일히 더하지 않고 파스칼 삼각형의 특성을 이용하여 선형 시간에 구해야 한다. 이분탐색의 범위를 좁혀 최적화를 할 수 있고, $n \choose r$ 값을 구할 때도 최적화를 할 수 있고, 정삼각형 영역 안에 들어있는 수의 합을 구할 때도 캐싱을 통해 최적화를 할 수 있다. 자세한 최적화는 아래 첨부된 코드를 참고하자.

#include <bits/stdc++.h>
using namespace std;

typedef long long lld;

const lld INF = (lld)1e18 + 9;

lld C(lld n, lld r)
{
    if (n < 0 || r < 0 || r > n) return 0;
    r = min(r, n-r);
    if (r == 0) return 1;
    if (r == 1) return n;
    if (r == 2) return n <= 1414213562 ? n*(n-1)/2 : INF;
    if (r == 3) return n <= 1817121 ? n*(n-1)*(n-2)/6 : INF;
    if (r == 4) return n <= 69994 ? n*(n-1)*(n-2)/6*(n-3)/4 : INF;
    if (r == 5) return n <= 10373 ? n*(n-1)*(n-2)*(n-3)/24*(n-4)/5 : INF;
    if (r == 6) return n <= 2996 ? n*(n-1)*(n-2)*(n-3)*(n-4)/120*(n-5)/6 : INF;
    if (r == 7) return n <= 1262 ? n*(n-1)*(n-2)*(n-3)*(n-4)*(n-5)/720*(n-6)/7 : INF;
    if (r == 8) return n <= 672 ? n*(n-1)*(n-2)*(n-3)*(n-4)*(n-5)/720*(n-6)/7*(n-7)/8 : INF;

static bool calced;
    static lld _C[419][419];
    if (!calced){
        calced = 1;
        _C[0][0] = 1;
        for (int i=1;i<419;i++){
            _C[i][0] = 1;
            for (int j=1;j<=i;j++){
                _C[i][j] = _C[i-1][j]+_C[i-1][j-1];
                if (_C[i][j] >= INF) _C[i][j] = INF;
            }
        }
    }

return n <= 418 ? _C[n][r] : INF;
}

lld S(lld n, int r, int l)
{
    static lld _cache[419][32][61];
    if (n <= 418 && r <= 31 && l <= 60 && _cache[n][r][l]) return _cache[n][r][l];

lld ret = C(n, r);
    for (int i=1;i<l;i++){
        ret += C(n+l, r+i);
        if (ret >= INF){ ret = INF; break; }
    }

if (n <= 418 && r <= 31 && l <= 60) _cache[n][r][l] = ret;
    return ret;
}

int solve(lld K)
{
    if (K == 1) return -1;

set<pair<lld, lld>> ans;
    // size = 1
    for (int r=1;;r++){
        if (C(r<<1, r) > K) break;
        lld s = r<<1, e = K;
        while (s <= e){
            lld m = s+e >> 1;
            lld v = C(m, r);
            if (v < K) s = m+1;
            else if (v > K) e = m-1;
            else{
                ans.emplace(m, r);
                ans.emplace(m, m-r);
                break;
            }
        }
    }

static lld ubound[61][32];
    // size > 1
    for (int size=2;;size++){
        lld limit = K / ((1LL << size) - 1);
        if (!limit) break;
        for (int r=0;;r++){
            if (C(r<<1, r) > limit) break;
            if (!ubound[size][r]){
                lld s = r<<1, e = INF, t = INF;
                while (s <= e){
                    lld m = s+e >> 1;
                    lld v = S(m, r, size);
                    if (v < INF) s = m+1, t = m;
                    else e = m-1;
                }
                ubound[size][r] = t;
            }
            lld s = r<<1, e = min(K, ubound[size][r]);
            while (s <= e){
                lld m = s+e >> 1;
                lld v = S(m, r, size);
                if (v < K) s = m+1;
                else if (v > K) e = m-1;
                else{
                    ans.emplace(m, r);
                    ans.emplace(m, m-r);
                    break;
                }
            }
        }
    }
    return ans.size();
}

int main()
{
    int T;
    for (scanf("%d", &T);T--;){
        lld K; scanf("%lld", &K);
        printf("%d\n", solve(K));
    }
}

15. 낙하 데미지

2차원 평면에 $N$ 개의 수평 선분이 있다. 선분은 서로 만나지 않으며, 선분 $i$의 y좌표는 $y_i$, 양 끝 점은 $s_i$, $e_i$다. 땅은 $y=0$인 직선이다. 캐릭터는 한 선분 위에서 시작하여, 선분 위에서 좌우로 자유롭게 이동 가능하다. 그리고 선분의 한 위치에서 수직 낙하를 할 수 있는데, 낙하하면서 만나는 선분에 착지할 수 있고, 착지하지 않고 마저 낙하할 수도 있다. 캐릭터가 선분 $i$에서 낙하하기 시작하여 선분 $j$에 착지할 경우, $(y_i-y_j)^2+c_j$ 만큼의 낙하 데미지를 받는다. 캐릭터가 어떤 선분 위에 착지한 경우, 마찬가지로 그 선분에서 좌우로 자유롭게 이동할 수 있고, 선분 위의 원하는 위치에서 다시 낙하할 수 있다. 모든 $N$ 개의 선분에 대해 그 선분에서 시작하여 땅까지 낙하할 때, 받는 낙하 데미지의 최솟값을 구하는 문제다.

이 문제의 간단한 풀이는 $O(N^2)$ 시간복잡도를 가지는 DP다. 다음과 같은 DP 배열을 정의하자.

$$D_i = 선분\ i에서\ 시작한\ 캐릭터가\ 땅까지\ 도달할\ 때,\ 받는\ 낙하\ 데미지의\ 최솟값$$

땅을 선분 $0$이라고 할 때, 초기값은 $D_0 = 0$이다.

점화식은 다음과 같다.

$$D_i = \min(D_j + (y_i-y_j)^2 + c_j)\ (여기서\ j는\ 선분\ i에서\ 낙하하면서\ 만나는\ 모든\ 선분)$$

이는 선분들을 y좌표 순서대로 정렬한 뒤, 이중 for문을 통해 구현할 수 있다.

이때, 위의 점화식은 Convex Hull Optimization(Convex Hull Trick, CHT)이 가능한 점화식이다.

$$D_i = \min(D_j + y_j^2 + c_j - 2y_jy_i) + y_i^2$$

여기서 선분들이 y좌표 순서대로 정렬되어 있으니, $j$가 증가함에 따라 $y_j$도 증가하고, 마찬가지로 $i$가 증가함에 따라 $y_i$도 증가한다. 즉, 스택과 포인터 하나를 이용하여 선형 시간에 CHT를 할 수 있는 점화식 꼴이다.

만약 점화식에서 $j$가 $j < i$인 모든 $j$라면, CHT 연습 문제 수준의 문제일 것이다. 하지만, 점화식에서 $j$는 $j < i$이면서 선분 $i$의 x좌표 범위와 선분 $j$의 x좌표 범위가 겹쳐야 한다. 이를 해결하기 위해, Segment Tree를 활용해야 한다. Segment Tree의 각 정점에서 두 개의 CHT를 돌린다. 하나는 그 정점의 자식 정점에 추가된 모든 $j$에 대해 CHT를 가지고 있고, 다른 하나는 그 정점이 표현 하는 좌표 범위에 추가된 모든 $j$에 대해 CHT를 가지고 있는다.

CHT를 스택과 포인터 하나를 통해 선형 시간으로 구현하면, 전체 시간복잡도는 $O(N \lg N)$이 되어 100점을 받을 수 있다. 만약, CHT를 Lichao Tree 등으로 구현하여 $O(n \lg n)$ 시간으로 구현하면, 전체 시간복잡도는 $O(N \lg^2 N)$이 되어, $N \le 50\,000$인 서브태스크만 통과한다.

참고로 서브태스크2의 경우 모든 $c_i$가 $0$이기 때문에, 낙하하다가 만나는 선분에 무조건 착지하면 낙하 데미지를 최소로 할 수 있다. 선분의 양 끝 점에서 낙하하는 경우와 선분의 양 끝 점에 착지하는 경우에 대해서만 생각하면 되므로, 점화식에서 가능한 $j$는 최대 4개다. 이를 이용하여 $O(N^2)$ 시간복잡도를 가지는 DP를 $O(N)$에 구현할 수 있다. 이 경우도, 정렬 등 전처리 작업 때문에 전체 시간복잡도는 $O(N \lg N)$이 된다.

#include <bits/stdc++.h>
using namespace std;

#define MAXN 200005
typedef long long lld;
typedef __int128_t lll;

const lld INF = 1e18;
int N;
struct Z{
	int y, s, e, c, idx;
} A[MAXN];
lld ans[MAXN];

// min CHT
struct CHT{
	struct Line{
		int a; lld b;
		lld get(lld x)const{ return a*x+b; }
	};
	CHT(): pt(0) {
		arr.push_back({0, INF});
	}
	int pt;
	vector<Line> arr;
	void add(const Line &t){
		while (arr.size() > 1){
			{
				auto&& a = arr[arr.size()-2];
				auto&& b = arr[arr.size()-1];
				if ((lll)(a.b-b.b)*(b.a-t.a) > (lll)(b.b-t.b)*(a.a-b.a)) break;
			}
			arr.pop_back();
		}
		if (pt >= arr.size()) pt = arr.size()-1;
		arr.push_back(t);
	}
	lld get(lld x){
		while (pt+1 < arr.size()){
			lld ay = arr[pt].get(x), by = arr[pt+1].get(x);
			if (ay < by) break;
			pt++;
		}
		return arr[pt].get(x);
	}
};

struct SegmentTree{
	struct Node{
		Node(lld S, lld E): l(-1), r(-1) {}
		int l, r;
		CHT up, down;
	};
	const lld S, E, LS, LE;
	vector<Node> tree;
	SegmentTree(lld S, lld E, lld LS, lld LE): S(S), E(E), LS(LS), LE(LE) {
		tree.emplace_back(LS, LE);
	}
	void update(int now, lld s, lld e, lld l, lld r, const CHT::Line &t){
		if (e < l || s > r) return;
		tree[now].down.add(t);
		lld m = s+e >> 1;
		if (l <= s && e <= r){
			tree[now].up.add(t);
			return;
		}
		if (tree[now].l < 0){
			tree[now].l = tree.size();
			tree.emplace_back(LS, LE);
		}
		if (tree[now].r < 0){
			tree[now].r = tree.size();
			tree.emplace_back(LS, LE);
		}
		update(tree[now].l, s, m, l, r, t);
		update(tree[now].r, m+1, e, l, r, t);
	}
	void add(lld l, lld r, const CHT::Line &t){ update(0, S, E, l, r, t); }
	lld get(int now, lld s, lld e, lld l, lld r, lld x){
		lld ret = INF;
		if (e < l || s > r) return ret;
		ret = tree[now].up.get(x);
		if (l <= s && e <= r){
			// down
			ret = min(ret, tree[now].down.get(x));
			return ret;
		}
		lld m = s+e >> 1;
		if (tree[now].l >= 0) ret = min(ret, get(tree[now].l, s, m, l, r, x));
		if (tree[now].r >= 0) ret = min(ret, get(tree[now].r, m+1, e, l, r, x));
		return ret;
	}
	lld get(lld l, lld r, lld x){
		return get(0, S, E, l, r, x);
	}
};

int main()
{
	scanf("%d", &N);
	vector<int> XS;
	int LS = 0, LE = 0;
	for (int i=1;i<=N;i++){
		scanf("%d%d%d%d", &A[i].y, &A[i].s, &A[i].e, &A[i].c);
		XS.push_back(A[i].s);
		XS.push_back(A[i].e);
		A[i].idx = i;
		LE = max(LE, A[i].y);
	}
	sort(XS.begin(), XS.end());
	XS.erase(unique(XS.begin(), XS.end()), XS.end());
	for (int i=1;i<=N;i++){
		A[i].s = lower_bound(XS.begin(), XS.end(), A[i].s)-XS.begin()+1;
		A[i].e = lower_bound(XS.begin(), XS.end(), A[i].e)-XS.begin()+1;
	}
	sort(A+1, A+N+1, [](const Z &a, const Z &b){
		return a.y < b.y;
	});
	SegmentTree segtree(1, XS.size(), LS, LE);
	segtree.add(1, XS.size(), {0, 0});
	for (int i=1;i<=N;i++){
		ans[A[i].idx] = segtree.get(A[i].s, A[i].e, A[i].y)+(lld)A[i].y*A[i].y;
		segtree.add(A[i].s, A[i].e, {-2*A[i].y, ans[A[i].idx]+(lld)A[i].y*A[i].y+A[i].c});
	}
	for (int i=1;i<=N;i++) printf("%lld\n", ans[i]);
}

'해법' 카테고리의 다른 글

Nexon Youth Programming Challenge(NYPC) 2022 Round 2-A 풀이 (0)	2022.08.29
Google Code Jam 2022 Round 2 풀이 및 후기 (0)	2022.05.16
Nexon Youth Programming Challenge(NYPC) 2020 예선 풀이 (9)	2020.09.06
Google CodeJam 2019 Round 2 풀이 (1)	2019.05.21
2018년 아시아태평양 정보올림피아드 (APIO2018) 풀이 (1)	2018.05.17

공유하기 링크

페이스북
카카오스토리
트위터

공지사항

최근에 올라온 글

최근에 달린 댓글

Total

Today

Yesterday

링크

TAG more

« 2024/04 »
일	월	화	수	목	금	토
	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30

글 보관함

PS 이야기

티스토리 뷰