티스토리 뷰
오랜만에 풀이 및 후기 글을 적는다. Google Code Jam은 매년 꾸준히 참가해왔다. 그동안 PS 공부할 시간적 여유가 없어서, 참가만 해왔었고, 다행히 최근에는 육아휴직으로 시간이 생겨서 밀린 PS 공부를 했다. 주로 최근에 well-known이 된 알고리즘/자료구조들을 공부하고 익히는 시간이었다. 다만, 최근 Round 2 성적이 최근에 공부한 것을 감안했을 때 아쉬움이 많이 남는 결과라 현재 심경과 풀이를 정리할 겸 포스팅을 시작한다.
A. Spiraling Into Control
Spiral 모양의 $N \times N$ 크기의 행렬이 있을 때, 원하는 만큼 shortcut을 놓아 정확히 $K$ 번의 이동으로 출발점 $1$에서 도착점 $N^2$으로 가는 문제다.
Shortcut이 하나도 없을 때 이동하는 횟수는 $N^2-1$ 번이다. 즉, shortcut을 적절히 놓아 이동 횟수를 $N^2-1-K$ 만큼 줄이는 문제가 된다. 한 가지 관찰이 필요하다. 각 칸에 놓을 수 있는 shortcut은 최대 1개다. 어떤 칸에 shortcut을 놓을 수 있다면, 그 shortcut으로 인해 줄어드는 이동 횟수를 생각해보자. 다음 그림은 $5 \times 5$ 크기의 행렬에서 가능한 shortcut들이 모두 표시되어 있고, shortcut 마다 줄일 수 있는 이동 횟수 값도 같이 적혀있다.
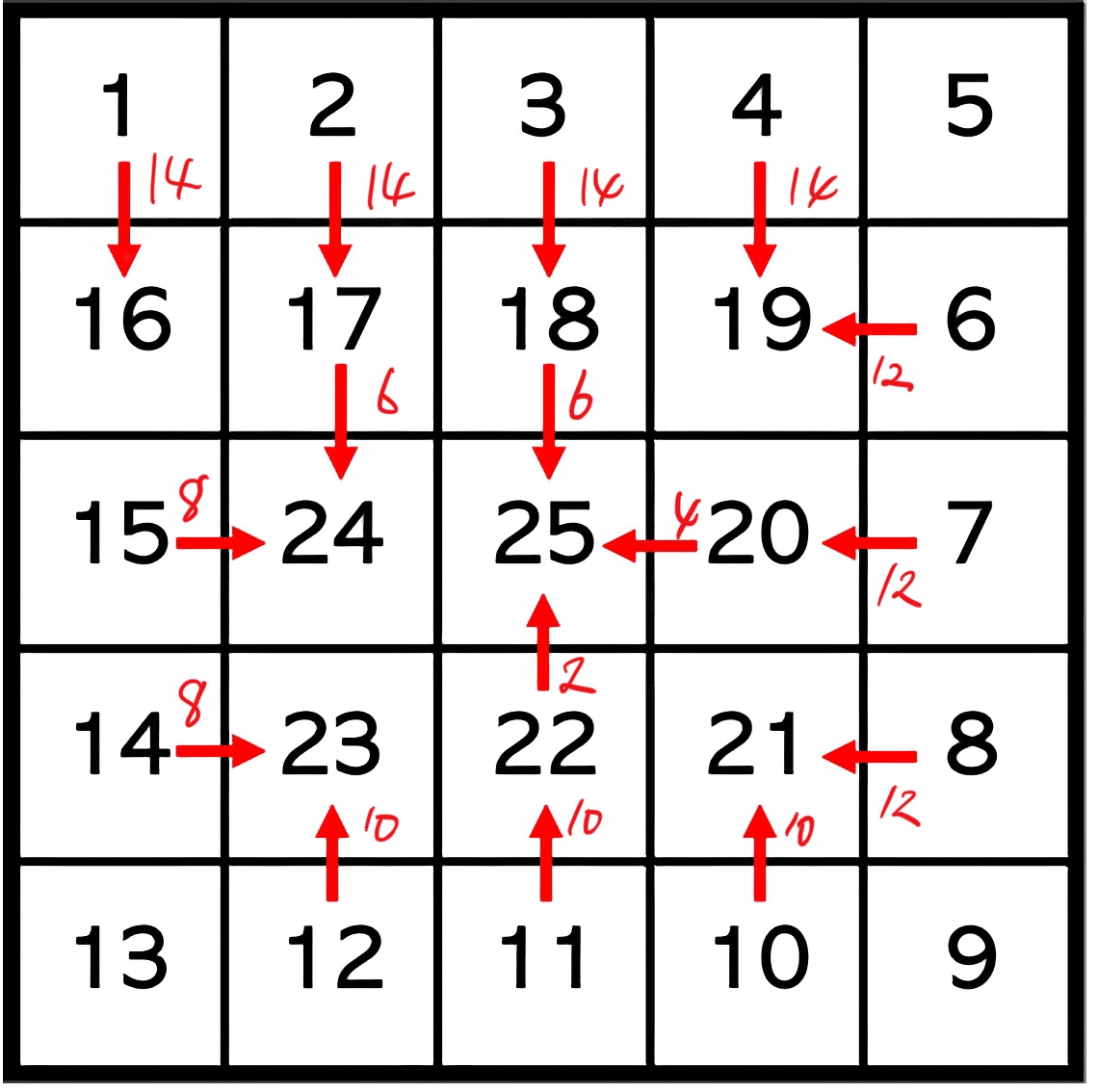
$N \times N$ 크기의 행렬에서 Shortcut은 이동 횟수를 $4N-6$ 줄이는 것부터 $2$ 만큼 줄이는 것까지 있다. 그리고 이동 횟수를 $k$ 만큼 줄이는 shortcut을 이용할 경우, 다음으로 이용 가능한 shortcut은 이동 횟수를 $k-8$부터 줄일 수 있다. 예를 들어, <그림 1>에서 이동 횟수를 14 만큼 줄이는 shortcut을 이용할 경우, 이동 횟수를 12, 10, 8 만큼 줄이는 shortcut은 이용할 수 없고, 이동 횟수를 6, 4, 2 만큼 줄이는 shortcut을 이용할 수 있다.
이를 기반으로, 줄여야 하는 이동 횟수 $X = N^2-1-K$가 있을 때, $2$ 이상 $4N-6$ 이하인 짝수 중 고른 수들의 차이가 8이상이 되도록 적절히 수를 골라서 합이 $X$가 되도록 만드는 문제가 되었다. 만약, $X$가 홀수라면 답은 IMPOSSIBLE이고, $X$가 짝수라면 $4N-6$부터 시작하여 그리디 하게 큰 수부터 고르면 된다. 마지막으로 실제 이용하는 shortcut은 가장 앞에 오는 shortcut만 이용하면 항상 가능하다는 것을 알 수 있다. 예를 들어, 위 그림에서 14를 골랐다면 (1, 16)인 shortcut을 항상 이용하고, 12를 골랐다면 (6, 19), 10은 (10, 21), 8은 (14, 23), 6은 (17, 24), 4는 (20,25), 2는 (22, 25)를 이용하면 된다. 시간복잡도는 $O(N)$이 된다.
B. Pixelated Circle
두 가지 방식으로 지름이 $R$인 원을 내부를 색칠하며 그린다. 두 방식에 대한 자세한 동작 과정은 본문에 의사 코드로 표현되어 있다. 한 방법은 draw_circle_filled(R)이고, 다른 방법은 draw_circle_filled_wrong(R)이다. 편의상 순서대로 옳은 방법, 틀린 방법이라고 표현하자. R이 주어졌을 때, 옳은 방법이 색칠하는 픽셀 수와 틀린 방법이 색칠하는 픽셀 수의 차이를 구하는 문제다.
이 문제는 실제로 옳은 방법과 틀린 방법을 $O(R^2)$ 시간복잡도로 구현하는 코드를 작성한 뒤, 몇 가지 특징들을 찾는 것이 중요하다.
특징 1. 틀린 방법이 색칠하는 모든 픽셀은 옳은 방법 또한 색칠한다.
때문에 우리는 옳은 방법은 색칠하지만 틀린 방법은 색칠하지 못하는 픽셀을 특정하면 된다. 또한, 답은 (옳은 방법이 색칠하는 픽셀 수)-(틀린 방법이 색칠하는 픽셀 수)가 된다.
특징 2. x = 0 혹은 y = 0인 픽셀에 대해 옳은 방법이 색칠하는 모든 픽셀을 틀린 방법 또한 색칠한다.
특징 3. 1사분면에 대해 답을 구하고 *4를 하면 답이 된다.
두 가지 방법 모두 색칠하는 픽셀이 x축 대칭, y축 대칭이 되므로 1 사분면에 대해 답을 구하면 전체 답을 구할 수 있다.
특징 4. 1사분면에 색칠되는 픽셀들은 $y = x$ 직선을 기준으로 대칭이다.
즉, 색칠 되는 픽셀 중 $x \leq y$인 것의 개수를 구하면, 1 사분면에 색칠되는 픽셀의 수를 구할 수 있다.
특징 5. 틀린 방법이 호출하는 함수 draw_circle_perimeter(r)은 서로 다른 r1, r2에 대해 색칠하는 픽셀이 항상 겹치지 않는다.
즉, 0 이상 $R$인 $r$에 대해 draw_circle_perimeter(r)이 색칠하는 픽셀 수를 모두 더하면 틀린 방법이 색칠하는 픽셀 수가 된다.
특징 6. draw_circle_perimeter(r)이 1사분면에 색칠하는 픽셀 중 $x \le y$인 픽셀들은 모두 $x$ 좌표가 서로 다르고, 한 $x$ 좌표에 대해 정확히 한 픽셀이 색칠된다.
이를 이용하여 draw_circle_perimeter(r)이 1사분면에 색칠하는 픽셀의 수를 빠른 시간 안에 구할 수 있다.
이 중 몇 가지는 수학적으로 증명이 비교적 간단하게 가능하고, 몇 가지는 수학적 증명보다 관찰과 코드를 통해 맞는지 확인하는 것이 좋다. 이 중 특징 4, 5, 6은 Test set 2를 푸는데 반드시 필요하다. 옳은 방법이 색칠하는 픽셀 개수를 $O(R)$ 혹은 $O(R \lg R)$ 시간복잡도로 세는 것은 간단하니 생략하고, 틀린 방법이 색칠하는 픽셀 개수를 구하는 방법에 대해 조금 짚어보겠다. 즉, 0 이상 $R$ 이하인 $r$에 대해 draw_circle_perimeter(r)가 색칠하는 픽셀 수를 구하면 되는데, 특징 6을 이용할 것이다. $x \leq y$를 만족하는 가장 큰 $x$를 구하면 색칠된 픽셀의 개수를 구할 수 있다. 이 가장 큰 $x$는 $r \cos(45^\circ)$ 근처가 된다. 그러나 이를 이분 탐색으로 $O(\lg r)$ 시간에 구해도 문제를 해결할 수 있다.
첨부된 코드는 소수점 연산등을 크게 고민하지 않아도 되는 $O(R \lg R)$ 시간복잡도를 가지는 방법이다.
C. Saving the Jelly
$N$ 명의 학생이 2차원 평면 위에 있고, $N+1$ 개의 사탕이 2차원 평면 위에 있다. 코치는 자신이 원하는 순서대로 학생을 호명하는데, 호명된 학생은 자신과 가장 가까운 사탕을 가지고 집으로 돌아간다. 만약, 가장 가까운 사탕이 여러 가지인 경우 코치는 그중 학생이 가져갈 사탕을 고른다. $N+1$ 개의 사탕 중 사탕 $1$은 코치 자신이 가지고 싶은 사탕이다. 이때, 적절한 순서로 학생들을 호명하여 아무도 사탕 $1$을 가져가지 못하게 하는 문제다.
우선, 답이 존재하는 필요 조건을 생각해보자. 모든 학생은 사탕 $1$보다 거리가 가까운 사탕 혹은 사탕 $1$과 거리가 같은 사탕을 가져가야 한다. 때문에 이분 매칭으로 왼쪽은 $N$ 명의 학생, 오른쪽은 사탕 $1$을 제외한 $N$ 개의 사탕을 놓고, 만약 학생 $i$와 사탕 $1$과의 거리가 사탕 $j$과의 거리보다 같거나 멀면 $i$에서 $j$로 가는 간선을 만들어준다. 이때, 답이 존재하기 위한 필요조건은 완전 매칭(perfect matching)이 존재하는 것이다.
여기까지만 생각했을 때, 완전 매칭이 존재하는 것은 필요 조건이지 충분조건이 아니다. 그런데, 임의의 완전 매칭이 있을 때 답을 항상 구할 수 있음을 보이면서 이 조건이 필요충분조건임을 같이 증명할 것이다.
우선 임의의 완전매칭을 구한다. 현재 상황에서, 남은 사탕 중에 어떤 학생 $i$와 제일 가까운 사탕이 $j$이고 완전 매칭에서 $i$와 $j$가 매칭 되어있다면, 학생 $i$가 호명되어 사탕 $j$를 가져가면 된다. 이제 이러한 학생이 한 명도 없을 때 완전 매칭을 적절히 바꾸어 이런 학생이 생기도록 항상 만들 수 있음을 보이겠다. 어떤 학생 $s_1$과 가장 가까운 사탕은 $c_1$이고, 완전 매칭에서 $c_1$은 $s_2$와 매칭 되어 있다. 마찬가지로 $s_2$와 가장 가까운 사탕은 $c_2$고, 완전 매칭에서 $c_2$은 $s_3$과 매칭 되어 있다. $s_3$와 가장 가까운 사탕은 $c_3$이고, 완전 매칭에서 $c_3$은 $s_1$과 매칭 되어 있다. 이러한 사이클을 우리는 항상 찾을 수 있고, 이러한 사이클을 찾은 경우, $s_1$을 $c_1$과, $s_2$는 $c_2$와, $s_3$은 $c_3$과 재매칭 시킬 수 있다. 아래 <그림 2>를 참고하자. 즉, 임의의 사이클을 찾은 뒤 이러한 재매칭 작업을 통해 어떤 학생 $i$와 가장 가까운 사탕 $j$를 매칭 시킬 수 있다. 이 과정을 반복하여 문제에서 요구하는 답을 항상 구할 수 있다. 동시에 위에서 말한 필요조건이 필요충분조건임을 증명했다.

이러한 방식으로 문제를 해결하면 완전매칭을 Hopcroft-Karp로 구하는데 $O(N^2\sqrt{N})$ 시간이 걸리고, 구한 완전 매칭에서 문제에서 요구하는 답을 구하는데 $O(N^2)$ 시간이 걸린다.
D. I, O Bot
일차원 좌표 공간에 로봇이 하나 있고, 물건이 $N$ 개 있다. 물건은 종류 $0$ 또는 종류 $1$이다. 로봇에는 종류 $0$인 물건 한 개를 담을 수 있는 공간, 종류 $1$인 물건 한 개를 담을 수 있는 공간이 있다. 로봇이 왼쪽 혹은 오른쪽으로 한 칸 움직일 때 필요한 비용은 $1$이고, 현재 위치에 있는 물건을 공간에 담는 비용은 $0$이다. 다만, 물건을 담을 공간이 이미 차있는 경우 물건을 다른 종류로 바꿀 수 있는데, 물건의 종류를 바꾸는 비용은 $C$다. 로봇은 좌표 $0$에 도달했을 때 담은 물건을 내려놓을 수 있는데, 내려놓는 비용은 $0$이다. 로봇이 좌표 $0$에서 시작하여, 모든 물건을 좌표 $0$에 옮길 때 필요한 최소 비용을 구하는 문제다.
물건의 좌표는 양수와 음수 모두 가능하다. 양수 좌표에 있는 물건들만 있다고 생각하고 문제를 해결하고, 음수 좌표에 있는 물건들만 있다고 생각하고 문제를 해결하여 둘의 결과값을 더하면 전체 결과가 된다.
Test set 1
$O(N^2)$ 시간복잡도를 가지는 DP로 해결할 수 있다. 다음과 같이 DP 배열을 정의하자.
D[i][j] = 종류 $0$인 물건 i개, 종류 $1$인 물건 j개를 원점에 가져다 놓을 때 필요한 최소 비용
여기서, 종류 $0$인 물건 i개란, 좌표가 순으로 정렬했을 때 앞에 오는 물건 i개를 의미한다. 즉, 같은 종류의 물건이 여러 개 있는 경우 원점과 가까운 물건을 먼저 옮기는 것이 더 유리하다.
여기서 다음 상황으로 가능한 것은 크게 3가지가 있다.
1) 물건을 1개만 담아 원점으로 돌아오는 경우
원점에서 출발하여 한 물건을 담고 다시 원점으로 돌아와 내려놓는다. 이때, 담는 물건은 종류 $0$ 남은 물건 중 가장 원점과 가까운 물건이거나 종류 $1$ 남은 물건 중 가장 원점과 가까운 물건이다.
2) 종류 $0$인 물건 하나, 종류 $1$인 물건 하나를 담아 원점으로 돌아오는 경우
종류 $0$인 남은 물건 중 가장 원점과 가까운 물건, 종류 $1인 남은 물건 중 가장 원점과 가까운 물건을 담고 원점으로 돌아와 내려놓는다.
3) 같은 종류의 물건을 2개 담아 원점으로 돌아오는 경우
일반성을 잃지 않고 종류 $0$인 물건 2개를 담고 돌아온다고 하자. 종류 $0$인 남은 물건 중 원점과 가장 가까운 물건 2개를 담는데, 그중 하나는 비용 $C$를 들여 종류 $1$로 바꾸고 담는다. 그리고 원점으로 돌아와 내려놓는다.
3가지 경우 각각에 대하여 뿌려주는 형태의 DP를 통해 쉽게 문제를 해결할 수 있다.
Test set 2
이 문제를 해결하기 위해서 조금 다른 DP를 써야 한다. 물건들이 종류 상관없이 위치를 기준으로 정렬되어 있다고 가정하고, 다음과 같이 DP 배열을 정의하자.
D[i] = 왼쪽 $i$ 개 물건을 원점에 가져다 놓을 때 필요한 최소 비용
초기 조건으로는 D[0] = 0, D[1] = 2*X[1]이 된다. 이제 D[i]를 계산하는 점화식을 구할 차례다. 일반성을 잃지 않고 $i$ 번째 물건의 종류는 $0$이라고 가정하자. 어떤 물건 둘을 한 번의 왕복에서 같이 로봇에 담아 원점으로 옮길 경우 두 물건을 매칭 된다고 표현하자. 이제 다음과 같이 경우를 크게 세 가지로 나눌 수 있다.
1) $i$ 번째 물건이 매칭되지 않는 경우
이 경우 최소 비용은 D[i-1]+2*X[i]가 된다.
2) $i$ 번째 물건이 매칭되는데, $i-1$ 번째 물건이 종류 $1$인 경우
이 경우 $i$ 번째 물건은 $i-1$ 번째 물건과 매칭 되는 것이 항상 좋다. 즉, 최소 비용은 D[i-2]+2*X[i]가 된다.
3) $i$ 번째 물건이 매칭되는데, $i-1$ 번째 물건이 종류 $0$인 경우
3-1) $i$ 번째 물건이 종류 $0$인 물건과 매칭 되는 경우
이 경우도 2)와 마찬가지로 $i$ 번째 물건은 $i-1$ 번째 물건과 매칭 되는 것이 항상 좋다. 즉, 최소 비용은 D[i-2]+2*X[i]+C가 된다.
3-2) $i$ 번째 물건이 종류 $1$인 물건과 매칭되는 경우
마지막으로, 생각하기 가장 까다로운 경우다. $i$ 번째 물건과, $i-1$ 번째 물건이 모두 종류 $0$이면서, $i$ 번째 물건은 종류 $1$인 물건과 매칭 되는 경우다. $i$ 번째 물건보다 왼쪽에 있으면서 가장 가까운 종류 $1$인 물건을 $j$ 번째 물건이라고 하자. 즉, $j+1, j+2, \cdots, i$ 번째 물건 모두 종류 $0$이다. 이때, 몇 가지 관찰이 필요한데 바로 왼쪽 $i$ 개 물건을 원점에 가져다 놓는 최적의 매칭이 존재하고, 최적의 매칭에서 $i$ 번째 물건이 종류 $1$인 물건과 매치가 되었다면, $i$ 번째 물건은 $j$ 번째 물건과 매칭이 되어야 하고, $i-1$ 번째 물건 또한 종류 $1$인 물건과 매치되어야 한다. 두 가지 모두 귀류법으로 어렵지 않게 증명 가능하다. 이제 이 명제를 연쇄적으로 적용할 수가 있는데, $i$ 번째 물건은 $j$ 번째 물건과 매칭 시키고, $i-1$ 번째 물건은 남은 종류 $1$인 물건 중 가장 오른쪽에 있는 물건과 매칭이 된다. 이 상황을 그림으로 나타내면 다음과 같다.

$k+1$ 번째 물건부터 $i$ 번째 물건까지 종류 $0$인 물건 개수와 종류 $1$인 물건 개수가 같은 가장 큰 $k$를 찾는다. 이때, $k+1$ 번째 물건부터 $i$ 번째 물건 사이에 있는 물건들은 서로 다른 종류끼리 매칭되는 것이 최적이며, 다음과 같이 매칭 됨을 알 수 있다. 즉, 최소 비용은 D[k]+(종류 $0$인 물건들의 위치 합에 2를 곱한 것)이다.
실제로 코딩할 때 3-2)와 2)는 한번에 고려해줄 수 있다. 이와 같이 DP를 하게 되면 DP 시간복잡도는 $O(N)$이며, 처음에 물건들을 위치를 기준으로 정렬해야 하므로, 전체 시간복잡도는 $O(N \lg N)$이 된다.
후기

우선 A가 빠른 시간 안에 풀기 어려운 문제였다. 어떻게든 간단하게 해결하는 방법을 찾으려고 노력하다가 결국 30분에 해결했다. 이때부터 뭔가 말릴 것 같은 느낌이 많이 들었다.
그리고 B를 읽었는데, 내가 좋아하지 않는 유형의 문제였고, 딱 봤을 때 풀이가 직관적으로 떠오르는 문제는 아니었다. $O(R^2)$ 코드를 짜고 정답에서 규칙이 있지 않을까 들여다봤고, 별다른 규칙이 떠오르지 않아서 B small만 풀고 C로 넘어갔다.
C도 풀이가 바로 떠오르지 않아서 small이라도 맞기 위해 brute force를 짰는데, TLE가 나왔다. 고민을 하던 중 완전 매칭 필요조건까지 찾았고, 완전매칭이완전 매칭이 존재하는 경우만 brute force를 돌렸더니 small 통과했다. 이때, 완전 매칭이 존재하면 답이 항상 존재한다는 사실을 채점 결과를 통해 알게 되어서 풀이에 거의 접근을 다 했다. 그러나 정말 바보 같이 사이클의 크기가 2인 경우에 대해서만 재매칭을 시켜줬다. 반신반의로 제출했는데 여전히 small이 통과되어서 "혹시 이게 되나?"라는 생각으로 D로 넘어갔다. 시간은 30분이 남았다. (물론, 싸이클의 크기가 2보다 클 수 있으므로 틀린 풀이다.)
D small 풀이는 어렵지 않은 DP 연습 문제 수준이었고, 30분 안에 충분히 풀 수 있었는데, 맨 처음에 접근을 잘못했고, 올바른 풀이가 떠올랐지만 시간이 10분 정도 남았다. 10분 안에 코딩하면 됐는데, 그냥 자포자기 상태였던 것 같다.
대회를 진행하면서 시간이 부족한 경우는 정말 오랜만이었다. 이전 라운드에서는 주어진 시간 안에 풀 수 있는 문제, 풀어야 하는 문제는 여유롭게 풀었던 것 같다. A를 푸는데 내가 계획했던 것보다 오래 걸렸던 것부터 말리기 시작하더니, B가 좋아하지 않는 유형의 문제라 자포자기 상태가 되어버린 것 같다. C는 풀이에 접근할 수 있는 충분한 단서가 주어졌음에도 불구하고, 이성적이었다면 접근할 수 있는 풀이를 접근하지 못했고, D small도 주어진 짧은 시간 안에 빠르게 코딩할 수 있었을 텐데, 손이 안 갔다. 대회 다음 날 다시 풀어보는데 아쉬움이 많이 남았다.
내가 스스로 생각했을 때 다음과 같은 결과를 받았으면 좋았을 것 같다:
A: 15분 정도에 해결
B: 빠르게 small 해결하고 C로 넘어가거나, 운이 좋아서 특징들을 발견하고 large까지 해결
C: 시간이 오래 걸리더라도 large까지는 해결
D: 빠르게 small 해결하고 large 손절, B large에 시간 투자
그러면 64점 혹은 80점으로 대회를 마치고 아쉬움이 크지 않았을 것 같다.
'해법' 카테고리의 다른 글
| Nexon Youth Programming Challenge(NYPC) 2022 Round 2-B 풀이 (354) | 2022.09.03 |
|---|---|
| Nexon Youth Programming Challenge(NYPC) 2022 Round 2-A 풀이 (11) | 2022.08.29 |
| Nexon Youth Programming Challenge(NYPC) 2021 예선 풀이 (3) | 2021.08.28 |
| Nexon Youth Programming Challenge(NYPC) 2020 예선 풀이 (9) | 2020.09.06 |
| Google CodeJam 2019 Round 2 풀이 (1) | 2019.05.21 |
- Total
- Today
- Yesterday
- USACO
- TRIE
- majority
- BOI 2009
- HackerRank
- optimization
- dynamic programming
- idea
- Dijkstra
- ioi
- BOI
- Dynamic Pramming
- Knuth Optimization
- Divide & Conquer
- Tree
- IOI2014
- Boyer-Moore Majority Vote Algorithm
- IOI2011
- Boyer
- moore
- IOI2012
- BOI 2001
- Splay Tree
- Parametric Search
- Segment tree
- Algorithm
- Greedy Method
- z-trening
- IOI2013
- vote
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
